题目内容
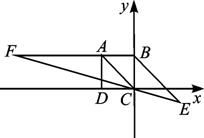
已知ABCD是正方形，BE∥AC,AC=CE,EC的延长线交BA的延长线于F，求证：AF=AE.
证明：如图，以CD所在直线为x轴，以C点为原点建立坐标系.设正方形的边长为1，则A（-1，1），B（0，1），若E点坐标为（x,y）,则
=（x,y-1）,
=(1,-1),
∵
∥
,∴x×(-1)-1×(y-1)=0.
又AC=CE及A（-1，1），C（0，0），E（x,y），可得x2+y2=2,∴解得E（
,
）,
=（
,
）.
又设F（x1,1）,则由
=（x1,1）和
=（
,
）共线，得x=-2-
,即F（-2-
,1）, 
=(-1-
,0),∴|
|=|
|=
+1,即AF=AE.
练习册系列答案
名校课堂系列答案
相关题目
已知ABCD是正方形，直线AE⊥平面ABCD，且AB=AE=1，
如图所示，已知ABCD是正方形，PD⊥平面ABCD，PD=AD=2．
如图，已知ABCD是正方形，DE⊥平面ABCD，BF⊥平面ABCD，且AB=FB=2DE．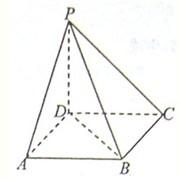
如图所示，已知ABCD是正方形，边长为2，PD⊥平面ABCD．