题目内容
已知椭圆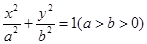 的左焦点
的左焦点 ,
,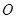 为坐标原点,点
为坐标原点,点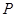 在椭圆上,点
在椭圆上,点 在椭圆的右准线上,若
在椭圆的右准线上,若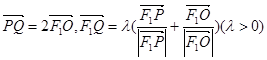 ,则椭圆的离心率为 .
,则椭圆的离心率为 .
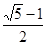
解析试题分析:因为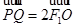 ,所以
,所以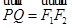 ,又因为
,又因为 表示与
表示与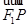 同向的单位向量,所以
同向的单位向量,所以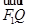 在
在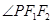 的平分线上,所以四边形
的平分线上,所以四边形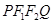 为菱形,所以
为菱形,所以 ,设点
,设点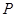
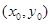 ,因为点
,因为点 在椭圆的右准线上,则点
在椭圆的右准线上,则点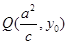 ,因为
,因为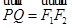 ,所以
,所以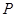
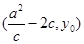 ,由因为
,由因为 ,所以
,所以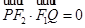 ,代入坐标进行运算,结合
,代入坐标进行运算,结合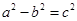 ,可以计算出椭圆的离心率为
,可以计算出椭圆的离心率为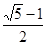 .
.
考点:本小题主要考查向量数量积的坐标运算、椭圆上点的性质和椭圆基本性质的应用,考查学生分析问题、解决问题的能力和数形结合思想的应用.
点评:解决本题的关键在于发现四边形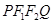 为菱形,所以对角线互相垂直,从而转化成向量的数量积为0进行求解,本题运算量比较大,求解时要仔细.
为菱形,所以对角线互相垂直,从而转化成向量的数量积为0进行求解,本题运算量比较大,求解时要仔细.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
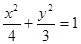 的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是
的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是  且与双曲线
且与双曲线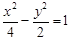 有相同渐近线方程的双曲线的标准方程为 .
有相同渐近线方程的双曲线的标准方程为 . 的离心率为
的离心率为 ,且双曲线的一个焦点恰好是抛物线
,且双曲线的一个焦点恰好是抛物线 的
的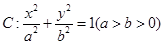 和圆
和圆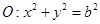 ,若
,若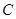 上存在点
上存在点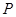 ,使得过点
,使得过点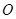 的两条切线,切点分别为
的两条切线,切点分别为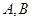 ,满足
,满足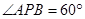 ,则椭圆
,则椭圆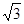 ) ,渐近线方程为
) ,渐近线方程为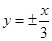 ,则此双曲线的方程为 _.
,则此双曲线的方程为 _.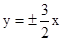 ,则其离心率是为 .
,则其离心率是为 .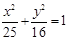 的长轴
的长轴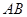 分成
分成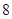 等份,过每个分点作
等份,过每个分点作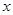 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于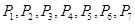 七个点,
七个点,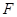 是椭圆的一个焦点则
是椭圆的一个焦点则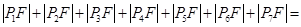 ________________
________________