题目内容
(本小题满分12分)设等差数列 的前
的前 项和为
项和为 .数列
.数列 的前
的前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(Ⅰ) ;
; (Ⅱ)
(Ⅱ) .
.
【解析】
试题分析:(1)根据等差数列的首项和公差求通项公式;(2)给出 与
与 的关系,求
的关系,求 ,常用思路:一是利用
,常用思路:一是利用 转化为
转化为 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为 的递推关系,先求出
的递推关系,先求出 与
与 的关系,再求
的关系,再求 ;由
;由 推
推 时,别漏掉
时,别漏掉 这种情况,大部分学生好遗忘;(3)因为数列中
这种情况,大部分学生好遗忘;(3)因为数列中 是奇数,偶数其通项公式不同,所以应用分类讨论的思想
是奇数,偶数其通项公式不同,所以应用分类讨论的思想
试题解析:( 12分)【解析】
(Ⅰ)由题意, ,得
,得 . 3分
. 3分
 ,
, ,
,
 ,两式相减,得
,两式相减,得
数列 为等比数列,
为等比数列, . 6分
. 6分
(Ⅱ) .
.
当 为偶数时,
为偶数时,
 . 9分
. 9分
当 为奇数时,
为奇数时,

 . 11分
. 11分
 . 12分
. 12分
考点:求数列的通项公式及前 项和
项和

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
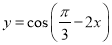 的图象向右平移
的图象向右平移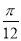 ,得到函数
,得到函数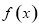 的图象,则函数
的图象,则函数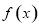 为( )
为( )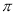 的奇函数 B.周期为
的奇函数 B.周期为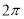 的奇函数 D.周期为
的奇函数 D.周期为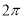 的偶函数
的偶函数 (
( ,
, ,
, )的部分图象如图所示,则
)的部分图象如图所示,则 ( )
( )
 B.
B. C.
C. D.
D.
 恒成立,则实数
恒成立,则实数 的取值范围为 .
的取值范围为 . 在复平面内对应的点的坐标为( )
在复平面内对应的点的坐标为( ) B.
B. C.
C. D.
D.

 的图象可能是
的图象可能是
 是自然对数的底数,函数
是自然对数的底数,函数 的零点为
的零点为 ,函数
,函数 的零点为b,则下列不等式成立的是
的零点为b,则下列不等式成立的是



 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为 的正方形
的正方形 和
和 ,点
,点 是边
是边 上的一个动点,设
上的一个动点,设 ,则
,则 .此时
.此时 = .
= .