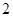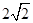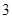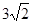题目内容
已知椭圆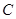 :
: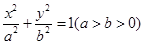 的离心率为
的离心率为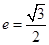 ,且过点
,且过点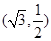 .
.
(Ⅰ)求椭圆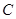 的标准方程;
的标准方程;
(Ⅱ)垂直于坐标轴的直线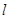 与椭圆
与椭圆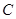 相交于
相交于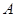 、
、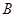 两点,若以
两点,若以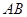 为直径的圆
为直径的圆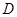 经过坐标原点.证明:圆
经过坐标原点.证明:圆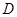 的半径为定值.
的半径为定值.
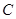 :
: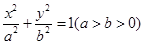 的离心率为
的离心率为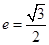 ,且过点
,且过点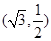 .
.(Ⅰ)求椭圆
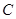 的标准方程;
的标准方程;(Ⅱ)垂直于坐标轴的直线
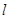 与椭圆
与椭圆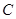 相交于
相交于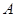 、
、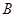 两点,若以
两点,若以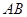 为直径的圆
为直径的圆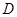 经过坐标原点.证明:圆
经过坐标原点.证明:圆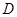 的半径为定值.
的半径为定值.(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
(I)由e和经过点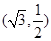 ,可建立关于a,b的方程,解方程组可求出a,b的值.问题得解.
,可建立关于a,b的方程,解方程组可求出a,b的值.问题得解.
(II)要考虑两种情况,一种是直线斜率不存在的情况,然后把以AB为直径的圆过原点,转化为 ,进而得到
,进而得到 ,证明O到直线AB的距离是定值即可.
,证明O到直线AB的距离是定值即可.
另一种是直线与x轴平行.作法同上
(Ⅰ) 2分
2分
 5分
5分
(Ⅱ)证明:设


 ,此时0到AB的距离为
,此时0到AB的距离为 9分
9分

同理可求得 综上所述,圆D的半径为定值
综上所述,圆D的半径为定值
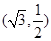 ,可建立关于a,b的方程,解方程组可求出a,b的值.问题得解.
,可建立关于a,b的方程,解方程组可求出a,b的值.问题得解.(II)要考虑两种情况,一种是直线斜率不存在的情况,然后把以AB为直径的圆过原点,转化为
 ,进而得到
,进而得到 ,证明O到直线AB的距离是定值即可.
,证明O到直线AB的距离是定值即可.另一种是直线与x轴平行.作法同上
(Ⅰ)
 2分
2分 5分
5分(Ⅱ)证明:设



 ,此时0到AB的距离为
,此时0到AB的距离为 9分
9分
同理可求得
 综上所述,圆D的半径为定值
综上所述,圆D的半径为定值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,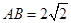 ,
,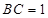 ,以
,以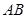 的中点
的中点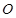 为
为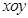 .
.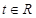 ,探究
,探究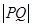 的最
的最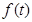 。
。
 ,
, 为坐标原点.
为坐标原点.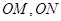 ,设
,设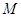 的横坐标为
的横坐标为 ,用
,用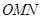 的面积,并求△
的面积,并求△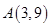 引圆
引圆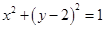 的两条切线
的两条切线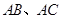 ,分别交抛物线于点
,分别交抛物线于点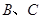 , 连接
, 连接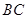 ,求直线
,求直线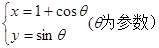 和直线
和直线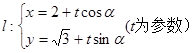
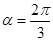 时,求圆上的点到直线
时,求圆上的点到直线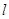 距离的最小值;
距离的最小值;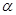 的取值范围.
的取值范围.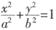 (a>b>0)的两个焦点,若椭圆上存在一点P使得
(a>b>0)的两个焦点,若椭圆上存在一点P使得 ,则椭圆的离心率e的取值范围为________.
,则椭圆的离心率e的取值范围为________.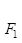 ,
,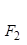 分别是椭圆E:
分别是椭圆E: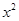 +
+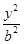 =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过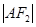 ,
,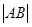 ,
,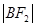 成等差数列。
成等差数列。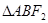 的周长
的周长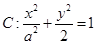 的焦点在
的焦点在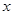 轴上,左、右顶点分别为
轴上,左、右顶点分别为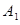 、
、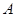 ,上顶点为
,上顶点为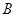 ,抛物线
,抛物线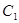 、
、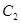 分别以
分别以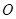 ,
,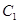 与
与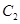 相交于直线
相交于直线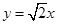 上一点
上一点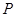 .
.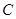 及抛物线
及抛物线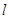 与直线
与直线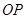 垂直,且与椭圆
垂直,且与椭圆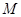 、
、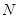 ,已知点
,已知点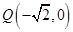 ,求
,求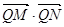 的最小值.
的最小值. 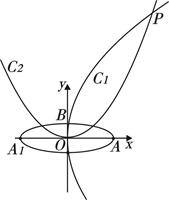
 :
: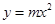 (
(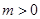 ),焦点为
),焦点为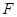 ,直线
,直线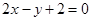 交抛物线
交抛物线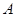 、
、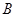 两点,
两点,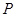 是线段
是线段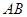 的中点,过
的中点,过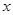 轴的垂线交抛物线
轴的垂线交抛物线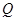 ,
,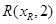 到焦点
到焦点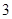 ,求此时
,求此时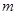 的值;
的值;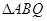 是以
是以
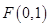 ,直线
,直线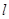 :
: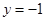 ,
,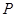 为平面上的动点,过点
为平面上的动点,过点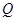 ,且
,且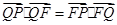 ,动点
,动点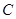 ,已知圆
,已知圆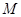 过定点
过定点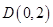 ,圆心
,圆心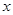 轴交于
轴交于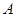 、
、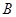 两点,设
两点,设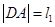 ,
,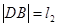 ,则
,则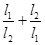 的最大值为( ▲ )
的最大值为( ▲ )