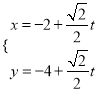题目内容

【题目】(1)从偶函数的定义出发,证明函数是偶函数的充要条件是它的图象关于y轴对称;

(2)从奇函数的定义出发,证明函数是奇函数的充要条件是它的图象关于原点对称.

【答案】(1)见解析(2)见解析

【解析】

先证明充分性，再证明必要性，即得证.

证明:(1)充分性:若的图象关于y轴对称,设为图象上任意一点,则M关于y轴的对称点仍在该图象上,即.

所以为偶函数,

必要性:若为偶函数,设为图象上任意一点,M关于y轴的对称点为,由于为偶函数,所以,所以在的图象上,所以的图象关于y轴对称.

(2)充分性:若的图象关于原点对称,设为其图象上任意一点,则M关于原点的对称点仍在该图象上,所以,所以为奇函数.

必要性:若为奇函数,设为其图象上任意一点,则M关于原点的对称点为,由于为奇函数,所以,所以仍在的图象上,所以的图象头于原点对称.

练习册系列答案
相关题目

【题目】在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：ρsin2θ＝2acos θ(a>0)，过点P(－2，－4)的直线l： (t为参数)与曲线C相交于M，N两点．

(1)求曲线C的直角坐标方程和直线l的普通方程；

(2)若|PM|，|MN|，|PN|成等比数列，求实数a的值．

【题目】已知中心在原点的椭圆的两焦点分别为双曲线的顶点，直线与椭圆交于、两点，且，点是椭圆上异于、的任意一点，直线外的点满足， ．　

（1）求点的轨迹方程；

（2）试确定点的坐标，使得的面积最大，并求出最大面积．

【题目】设函数，其中．

（1）讨论极值点的个数；

（2）设，函数，若，（）满足且，证明：．

【题目】设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x-85.71，则下列结论中不正确的是

A. y与x具有正的线性相关关系

B. 回归直线过样本点的中心（，）

C. 若该大学某女生身高增加1cm，则其体重约增加0.85kg

D. 若该大学某女生身高为170cm，则可断定其体重比为58.79kg

【题目】已知平面直角坐标系，以为极点，轴的非负半轴为极轴建立极坐标系，点的极坐标为，直线的极坐标方程为，曲线的参数方程为 （为参数）.

（1）写出点的直角坐标及曲线的直角坐标方程；

（2）若为曲线上的动点，求中点到直线的距离的最小值.

【题目】定于符号函数，已知，，

（1）求关于的表达式，并求的最小值；

（2）当时，函数在上有唯一零点，求的取值范围；

（3）已知存在，使得对任意恒成立，求的取值范围.

【题目】已知函数.

（1）当时，求证：；

（2）讨论函数的零点的个数。

【题目】已知函数， 为自然对数的底数， .

（1）试讨论函数的单调性；

（2）当时， 恒成立，求实数的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网