题目内容
已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求
(1)求异面直线BD与B1E所成角的大小;
(2)求四面体AB1D1C的体积.

(1)求异面直线BD与B1E所成角的大小;
(2)求四面体AB1D1C的体积.

(1)连接B1D1、D1E,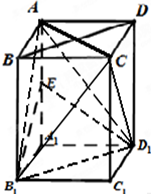
∵正四棱柱ABCD-A1B1C1D1中,B1B∥D1D且B1B=D1D
∴四边形BB1D1D是平等四边形
因此B1D1∥BD,可得∠EB1D1或其补角就是异面直线BD与B1E所成角
∵AA1=2AB=2,∴B1D1=ED1=B1E=
,得△B1D1E是等边三角形,∠EB1D1=60°
由此可得,异面直线BD与B1E所成角的大小为60°;
(2)根据题意,得V正四棱柱ABCD-A1B1C1D1=S正方形ABCD×AA1=2
∵V三棱锥B-ACB1=V三棱锥A1-AB1D1=V三棱锥C1-CB1D1=V三棱锥D-ACD1=
×
×1×1×2=
∴四面体AB1D1C的体积为
V=V正四棱柱ABCD-A1B1C1D1-(V三棱锥B-ACB1+V三棱锥A1-AB1D1
+V三棱锥C1-CB1D1+V三棱锥D-ACD1)=2-
=

∵正四棱柱ABCD-A1B1C1D1中,B1B∥D1D且B1B=D1D
∴四边形BB1D1D是平等四边形
因此B1D1∥BD,可得∠EB1D1或其补角就是异面直线BD与B1E所成角
∵AA1=2AB=2,∴B1D1=ED1=B1E=
| 2 |
由此可得,异面直线BD与B1E所成角的大小为60°;
(2)根据题意,得V正四棱柱ABCD-A1B1C1D1=S正方形ABCD×AA1=2
∵V三棱锥B-ACB1=V三棱锥A1-AB1D1=V三棱锥C1-CB1D1=V三棱锥D-ACD1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴四面体AB1D1C的体积为
V=V正四棱柱ABCD-A1B1C1D1-(V三棱锥B-ACB1+V三棱锥A1-AB1D1
+V三棱锥C1-CB1D1+V三棱锥D-ACD1)=2-
| 4 |
| 3 |
| 2 |
| 3 |

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目




 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成二面角的平面角的余弦值为
所成二面角的平面角的余弦值为 .
.
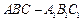 中,
中,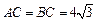 ,
,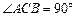 ,AA1=2,E、F分别是AC、AB的中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为
,AA1=2,E、F分别是AC、AB的中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为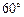 ,则截面的面积为____________.
,则截面的面积为____________.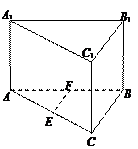
 .(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q=
.(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q= C1A1,求平面QDC与平面A1DC所成锐二面角的大小.
C1A1,求平面QDC与平面A1DC所成锐二面角的大小.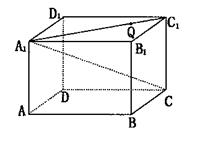



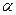 -
-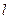 -
-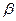 的棱
的棱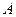 ,在平面
,在平面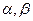 内各有一条射线
内各有一条射线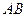 ,
,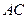 与
与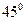 ,
,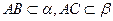 ,则
,则 。
。