题目内容
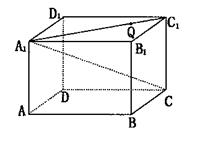
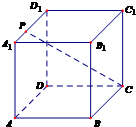
（本小题满分12分）在长方体ABCD—A1B1C1D1中，AA1=1，AD=DC=
.（1）求直线A1C与D1C1所成角的正切值；（2）在线段A1C上有一点Q，且C1Q=
C1A1，求平面QDC与平面A1DC所成锐二面角的大小.
.（1）求直线A1C与D1C1所成角的正切值；（2）在线段A1C上有一点Q，且C1Q=C1A1，求平面QDC与平面A1DC所成锐二面角的大小.（1）
（2）30°
（2）30°求线面角关键是作垂线，找射影，求异面直线所成的角采用平移法
求二面角的大小也可应用面积射影法，向量法办
解法一：（I）
为异面直线A
C与D1C所成的角
连AD，在Rt△ADC中，CD=，AD=2，
（II）过Q作EF（在平面AC内）使EF//AB， 
连B1C、CF、DF，（面EFCD即平面QDC；面A1B1CD即平面A1DC）
即为二面角A1—DC—Q的平面角.
~
. 
，即所求二面角大小为30°
解法二：（I）同解法一（I）
（II）建立空间直角坐标系，
即平面QDC与平面A1DC所成锐二面角为
。
求二面角的大小也可应用面积射影法，向量法办 解法一：（I）
为异面直线AC与D1C所成的角 连A
D，在Rt△ADC中，CD=，AD=2，（II）过Q作EF（在平面A
C内）使EF//AB， 连B1C、CF、DF，（面EFCD即平面QDC；面A1B1CD即平面A1DC）
即为二面角A1—DC—Q的平面角.
|
~. ，即所求二面角大小为30° 解法二：（I）同解法一（I）
（II）建立空间直角坐标系，
|
即平面QDC与平面A1DC所成锐二面角为
。
练习册系列答案
名题金卷系列答案
相关题目
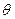，已知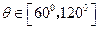
，则AC、BD之间的距离的最大值和最小值 ．
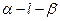为60°的二面角，等腰直角三角形MPN的直角顶点P在l上，M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.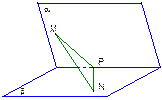
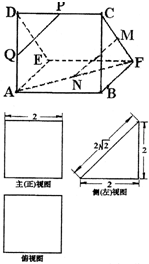
中，三条棱
、
、
两两互相垂直，且
是
边的中点，则
与平面
所成的角的大小是 （ 用反三角函数表示）；
的平面角为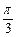
，AB⊥BC，BC⊥CD，
，BC在l上，
，若
，则AD的长为 .