Question

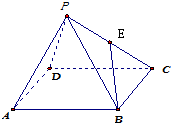
如图，在正方体ABCD-A₁B₁C₁D₁中，设AA₁=2．M，N分别是C₁D₁，CC₁的中点．
（1）求异面直线A₁N与MC所成角的余弦值；
（2）设P为线段AD上任意一点，求证：MC⊥PN．

Answer 1

（1）∵正方体ABCD-A₁B₁C₁D₁中，DA、DC、DD₁两两互相垂直，
∴以D为原点，分别以DA、DC、DD₁为x、y、z轴，建立如图空间直角坐标系
可得D（0，0，0），A（2，0，0），A₁（2，0，2），C（0，2，0），M（0，1，2），N（0，2，1）
∴向量

A1N

=（-2，2，-1），

MC

=（0，1，-2）
根据空间向量的夹角公式，得cos＜

A1N

，

MC

＞=

A1N • MC

| A1N |•| MC |

=

4 5

15

设异面直线A₁N与MC所成角为θ
可得cosθ=|cos＜

A1N

，

MC

＞|=

4 5

15

，即异面直线A₁N与MC所成角的余弦值为

4 5

15

；
（2）由（1）中所建立的坐标系，得
∵P为线段AD上任意一点，
∴设P（x，0，0），其中x∈[0，2]
可得

PN

=（-x，2，1）
∵

MC

=（0，1，-2），
∴

MC

•

PN

=0×（-x）+1×2+（-2）×1=0
由此可得

MC

⊥

PN

，即P为线段AD上任意一点，都有MC⊥PN成立．