题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)判断函数![]() 能否有3个零点?若能,求出
能否有3个零点?若能,求出![]() 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
【答案】(1)见解析;(2)不可能有![]() 个零点;说明见解析
个零点;说明见解析
【解析】
(1)求导后,根据导函数零点的分布情况在![]() 不同的取值范围情况下讨论导函数的正负,从而得到函数的单调性;(2)采用反证法,假设有
不同的取值范围情况下讨论导函数的正负,从而得到函数的单调性;(2)采用反证法,假设有![]() 个零点,可知需满足
个零点,可知需满足![]() 或
或![]() ;当
;当![]() 时,可得极大值
时,可得极大值![]() ,从而知不可能有
,从而知不可能有![]() 个零点;当
个零点;当![]() 时,可得极大值
时,可得极大值![]() ,将其看做关于
,将其看做关于![]() 的函数,通过导数可判断出
的函数,通过导数可判断出![]() ,从而可知不可能有
,从而可知不可能有![]() 个零点;可知假设错误,即
个零点;可知假设错误,即![]() 不可能有
不可能有![]() 个零点.
个零点.
(1)由题意知:函数定义域为![]()
![]()
①若![]() ,则
,则![]()
当![]() 时,
时,![]() ,则
,则![]() 为减函数
为减函数
当![]() 时,
时,![]() ,则
,则![]() 为增函数
为增函数
②若![]()
当![]() 或
或![]() 时,
时,![]() ,则
,则![]() 为增函数
为增函数
当![]() 时,
时,![]() ,则
,则![]() 为减函数
为减函数
③若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上增函数
上增函数
④若![]()
当![]() 或
或![]() 时,
时,![]() ,则
,则![]() 为增函数
为增函数
当![]() 时,
时,![]() ,则
,则![]() 为减函数
为减函数
(2)若函数![]() 有
有![]() 个零点,由(1)可知,必有
个零点,由(1)可知,必有![]() 或
或![]()
①若![]() ,由(1)可知
,由(1)可知![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值
处取得极小值
![]()
![]() 此时
此时![]() 不可能有
不可能有![]() 个零点
个零点
②若![]() ,由(1)可知
,由(1)可知![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值
处取得极小值
![]()
则![]() ,
,![]()
![]()
![]() ,即
,即![]()
![]() 在
在![]() 上单调递增
上单调递增
![]()
![]() 在
在![]() 上单调递减
上单调递减
当![]() 时,
时,![]()
![]()
![]() 此时
此时![]() 不可能有
不可能有![]() 个零点
个零点
综上所述:函数![]() 不可能有
不可能有![]() 个零点
个零点

【题目】有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如下:
甲公司 | 乙公司 | ||||||||
职位 | A | B | C | D | 职位 | A | B | C | D |
月薪/千元 | 5 | 6 | 7 | 8 | 月薪/千元 | 4 | 6 | 8 | 10 |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 |
(1)若两人分别去应聘甲、乙两家公司的C职位,记这两人被甲、乙两家公司的C职位录用的人数和为![]() ,求
,求![]() 的分布列;
的分布列;
(2)根据甲、乙两家公司的聘用信息,如果你是该求职者,你会选择哪一家公司?说明理由。
(3)若小王和小李分别被甲、乙两家公司录用,求小王月薪高于小李的概率。
【题目】一只药用昆虫的产卵数![]() 与一定范围内与温度
与一定范围内与温度![]() 有关, 现收集了该种药用昆虫的6组观测数据如下表:
有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求![]() 关
关![]() 的回归方程为
的回归方程为![]()
![]() 且相关指数
且相关指数![]()
( i )试与 (1)中的线性回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为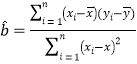 ,
,![]() ,相关指数
,相关指数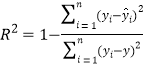 .
.
![]()
![]()
![]()
![]() 。
。