题目内容
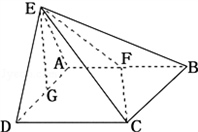
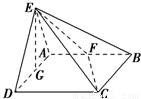 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角(1)求证:EG⊥平面ABCD;
(2)若AD=2,求二面角E-FC-G的度数;
(3)当AD的长是多少时,D点到平面EFC的距离为2?并说明理由.
【答案】分析:(1)由已知中,△ADE是等边三角形,G是AD的中点,结合等边三角形“三线合一”的性质,易得EG⊥AD,又由平面EAD⊥平面ABCD,由面面垂直的性质可得EG⊥平面ABCD;
(2)连接CG,则CG是EC在平面ABCD的射影,结合已知中EC与平面ABCD成30°角,得∠ECG=30°,解Rt△ECG,Rt△CDG,求出GF,FC,GC的长,易根据勾股定理得到,GF⊥FC,EF⊥FC,故∠EFG是二面角E-FC-G的平面角,解三角形EFG,即可求出二面角E-FC-G的度数.
(3)根据VE-DFC=VD-EFC,通过计算底面积,从而可求AD的长
解答: 解:(1)证明:如图所示,∵△ADE是等边三角形,
解:(1)证明:如图所示,∵△ADE是等边三角形,
∴EG⊥AD
又平面EAD平面ABCD且相交于AD,
∴EG⊥平面ABCD
(2)连接CG,则CG是EC在平面ABCD的射影
∴∠ECG是EC与平面ABCD所成的角,
∴∠ECG=30°
在Rt△ECG中:
∵AD=2,
∴EG= ,
,
∴CG=3
在Rt△CDG中:
∵DG=1,GC=3,
∴DC=
则AF=BF= ,GF=
,GF= ,FC=
,FC=
∴GF2+FC2=GC2,
即GF⊥FC
∵GF是EF在平面AC内的射影,
∴EF⊥FC
∴∠EFG是二面角E-FC-G的平面角.
在Rt△EGF中,EG=GF=
∴∠EFG=45°
故所求二面角E-FC-G的度数为45°
(3)设AD=2a,则可得 ,S△EFC=3a2
,S△EFC=3a2
∵VE-DFC=VD-EFC
∴
∴
∴
点评:本题考查的知识点是直线与平面垂直的判定,二面角的平面角的求法,求二面角的平面角,关键是要找出这个角,将空间求角问题,转化为解三角形问题.
(2)连接CG,则CG是EC在平面ABCD的射影,结合已知中EC与平面ABCD成30°角,得∠ECG=30°,解Rt△ECG,Rt△CDG,求出GF,FC,GC的长,易根据勾股定理得到,GF⊥FC,EF⊥FC,故∠EFG是二面角E-FC-G的平面角,解三角形EFG,即可求出二面角E-FC-G的度数.
(3)根据VE-DFC=VD-EFC,通过计算底面积,从而可求AD的长
解答:
 解:(1)证明:如图所示,∵△ADE是等边三角形,
解:(1)证明:如图所示,∵△ADE是等边三角形,∴EG⊥AD
又平面EAD平面ABCD且相交于AD,
∴EG⊥平面ABCD
(2)连接CG,则CG是EC在平面ABCD的射影
∴∠ECG是EC与平面ABCD所成的角,
∴∠ECG=30°
在Rt△ECG中:
∵AD=2,
∴EG=
 ,
,∴CG=3
在Rt△CDG中:
∵DG=1,GC=3,
∴DC=

则AF=BF=
 ,GF=
,GF= ,FC=
,FC=
∴GF2+FC2=GC2,
即GF⊥FC
∵GF是EF在平面AC内的射影,
∴EF⊥FC
∴∠EFG是二面角E-FC-G的平面角.
在Rt△EGF中,EG=GF=

∴∠EFG=45°
故所求二面角E-FC-G的度数为45°
(3)设AD=2a,则可得
 ,S△EFC=3a2
,S△EFC=3a2∵VE-DFC=VD-EFC
∴

∴

∴

点评:本题考查的知识点是直线与平面垂直的判定,二面角的平面角的求法,求二面角的平面角,关键是要找出这个角,将空间求角问题,转化为解三角形问题.

练习册系列答案
相关题目
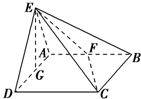 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角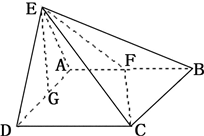
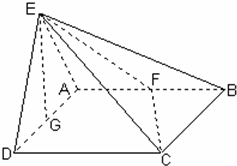 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角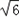 ,求三棱锥F﹣EGC的体积.
,求三棱锥F﹣EGC的体积.