题目内容
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,∠BCG=30°.
(1)求证:EG⊥平面ABCD
(2)若M,N分别是EB,CD的中点,求证MN∥平面EAD.
(3)若AD=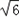 ,求三棱锥F﹣EGC的体积.
,求三棱锥F﹣EGC的体积.
(1)求证:EG⊥平面ABCD
(2)若M,N分别是EB,CD的中点,求证MN∥平面EAD.
(3)若AD=
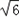 ,求三棱锥F﹣EGC的体积.
,求三棱锥F﹣EGC的体积. 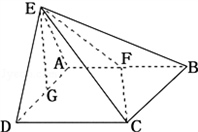
证明:(1)∵△ADE是正三角形,
∴EG⊥AD,
又平面ADE⊥平面ABCD,
且相交于AD,
∴EG⊥平面ABCD.
(2)取AE中点H,连接DH,
∵MH= AB,MH∥AB,即MH∥DN,MH=DN,
AB,MH∥AB,即MH∥DN,MH=DN,
∴四边形MHDN为平行四边形,
∴MN∥DH,
又MN 平面EAD,DH
平面EAD,DH 平面ADE,
平面ADE,
∴MN∥平面EAD.
(3)由(1)知EG⊥平面ABCD,
即底面CGF的高为EG,且GE= ,
,
又在直角三角形EGC中,
由GE= ,得CG=
,得CG=  ,
,
∴DC=2 .
.
∴S△CGF=2 ×
× ﹣
﹣ ×
×  ×2
×2 ﹣
﹣ ×
×  ×
×  =
=  ,
,
∴VF﹣EGC=VC﹣EGF = ×
×  ×
× =
=

∴EG⊥AD,
又平面ADE⊥平面ABCD,
且相交于AD,
∴EG⊥平面ABCD.
(2)取AE中点H,连接DH,
∵MH=
 AB,MH∥AB,即MH∥DN,MH=DN,
AB,MH∥AB,即MH∥DN,MH=DN,∴四边形MHDN为平行四边形,
∴MN∥DH,
又MN
 平面EAD,DH
平面EAD,DH 平面ADE,
平面ADE, ∴MN∥平面EAD.
(3)由(1)知EG⊥平面ABCD,
即底面CGF的高为EG,且GE=
 ,
,又在直角三角形EGC中,
由GE=
 ,得CG=
,得CG=  ,
, ∴DC=2
 .
. ∴S△CGF=2
 ×
× ﹣
﹣ ×
×  ×2
×2 ﹣
﹣ ×
×  ×
×  =
=  ,
, ∴VF﹣EGC=VC﹣EGF =
 ×
×  ×
× =
=


练习册系列答案
相关题目
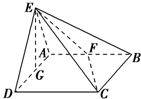 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角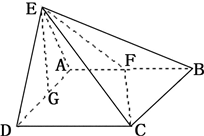
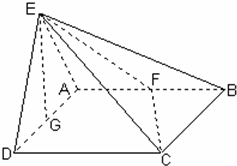 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角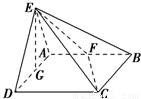 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成30°角