题目内容
(1)求经过点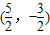 ,且与椭圆
,且与椭圆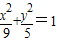 有共同焦点的椭圆方程;
有共同焦点的椭圆方程;(2)已知椭圆以坐标轴为对称轴,且长轴长是短轴长的3倍,点P(3,0)在该椭圆上,求椭圆的方程.
【答案】分析:(1)确定椭圆 的焦点坐标,利用椭圆的定义,可求椭圆方程;
的焦点坐标,利用椭圆的定义,可求椭圆方程;
(2)设出椭圆的右边方程,利用长轴长是短轴长的3倍,点P(3,0)在该椭圆上,即可求椭圆的方程.
解答:解:(1)由题意,椭圆 的焦点坐标为(±2,0),则
的焦点坐标为(±2,0),则
∵所求椭圆经过点 ,且与椭圆
,且与椭圆 有共同焦点
有共同焦点
∴c=2,2a= +
+ =2
=2
∴a= ,∴
,∴ =6,
=6,
∴椭圆的标准方程为 .
.
(2)设椭圆方程为Ax2+By2=1(A>0,B>0,A≠B).
∵点P(3,0)在该椭圆上,∴9A=1,即A= ,
,
又长轴长是短轴长的3倍,∴B=1或 ,
,
∴椭圆的方程为 或
或 .
.
点评:本题考查椭圆的标准方程,考查学生的计算能力,属于中档题.
 的焦点坐标,利用椭圆的定义,可求椭圆方程;
的焦点坐标,利用椭圆的定义,可求椭圆方程;(2)设出椭圆的右边方程,利用长轴长是短轴长的3倍,点P(3,0)在该椭圆上,即可求椭圆的方程.
解答:解:(1)由题意,椭圆
 的焦点坐标为(±2,0),则
的焦点坐标为(±2,0),则∵所求椭圆经过点
 ,且与椭圆
,且与椭圆 有共同焦点
有共同焦点∴c=2,2a=
 +
+ =2
=2
∴a=
 ,∴
,∴ =6,
=6,∴椭圆的标准方程为
 .
.(2)设椭圆方程为Ax2+By2=1(A>0,B>0,A≠B).
∵点P(3,0)在该椭圆上,∴9A=1,即A=
 ,
,又长轴长是短轴长的3倍,∴B=1或
 ,
,∴椭圆的方程为
 或
或 .
.点评:本题考查椭圆的标准方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 和椭圆E2:
和椭圆E2: 满足
满足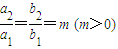 ,则称这两个椭圆相似,m称为其相似比.
,则称这两个椭圆相似,m称为其相似比. ,且与椭圆
,且与椭圆 相似的椭圆方程;
相似的椭圆方程; 的最大值和最小值;
的最大值和最小值;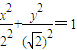 和C2:
和C2: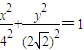 交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为
交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为 ”.请用推广或类比的方法提出类似的一个真命题,并给予证明.
”.请用推广或类比的方法提出类似的一个真命题,并给予证明.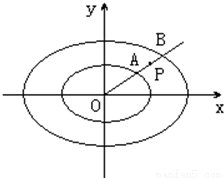
 和椭圆E2:
和椭圆E2: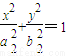 满足
满足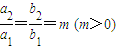 ,则称这两个椭圆相似,m称为其相似比.
,则称这两个椭圆相似,m称为其相似比.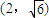 ,且与椭圆
,且与椭圆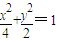 相似的椭圆方程;
相似的椭圆方程;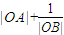 的最大值和最小值;
的最大值和最小值;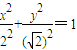 和C2:
和C2: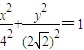 交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为
交于A、B两点,P为线段AB上的一点,若|OA|、|OP|、|OB|成等差数列,则点P的轨迹方程为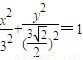 ”.请用推广或类比的方法提出类似的一个真命题,并给予证明.
”.请用推广或类比的方法提出类似的一个真命题,并给予证明.
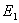 :
: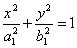 和椭圆
和椭圆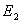 :
: 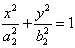 满足
满足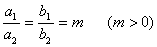 ,则称这两个椭圆相似,
,则称这两个椭圆相似,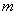 称为其相似比。
称为其相似比。 (1)求经过点
(1)求经过点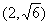 ,且与椭圆
,且与椭圆 相似
相似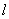 分别与(1)中的两个椭
分别与(1)中的两个椭 值。
值。