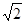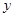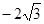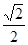题目内容
若椭圆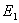 :
: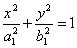 和椭圆
和椭圆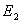 :
: 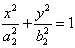 满足
满足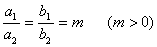 ,则称这两个椭圆相似,
,则称这两个椭圆相似,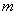 称为其相似比。
称为其相似比。
 (1)求经过点
(1)求经过点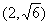 ,且与椭圆
,且与椭圆 相似
相似
的椭圆方程。
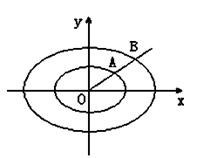
(2)设过原点的一条射线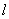 分别与(1)中的两个椭
分别与(1)中的两个椭
圆交于A、B两点(其中点A在线段OB上),
求 值。
值。
【答案】
解:(1)设所求的椭圆方程为 ,则有
,则有
 解得
解得
∴所要求的椭圆方程为
(2)①当射线与 轴重合时,
轴重合时, 2
2
②当射线不与坐标轴重合时,由椭圆的对称性,我们仅考察A、B在第一象限的情形。
设其方程为 (
( ),设
),设 ,
,
由 解得
解得

由 解得
解得

所以: 2
2

练习册系列答案
相关题目
.(本小题满分14分)
已知椭圆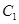 、抛物线
、抛物线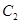 的焦点均在
的焦点均在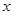 轴上,
轴上,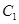 的中心和
的中心和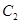 的顶点均为原点
的顶点均为原点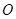 ,从每条曲
,从每条曲
线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(Ⅰ)求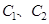 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线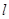 满足条件:①过
满足条件:①过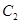 的焦点
的焦点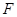 ;②与
;②与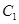 交不同两点
交不同两点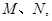 且满
且满
足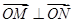 ?若存在,求出直线
?若存在,求出直线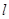 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
 2
2