题目内容
已知圆C:x2+y2=4和定点A(1,0),求经过点A且与圆C相切的动圆圆心M的轨迹方程.
思路解析:本题考查利用两圆位置关系的几何特征和定义法求动圆圆心的轨迹方程,可以把圆心的运动轨迹转化为已知曲线,进行求解.
解:设动圆圆心为M(x,y).因为圆M总过点A,所以|MA|=r(动圆半径).又圆M与圆C相切,根据实际情况判断只能内切.所以|MC|=2-|MA|,即|MC|+|MA|=2.所以M的轨迹是以C、A为焦点,长轴长为2的椭圆,其方程为 =1,即
=1,即![]() .
.

练习册系列答案
相关题目
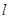 :x-y+2=0的对称点都在圆C上,则a=
.
:x-y+2=0的对称点都在圆C上,则a=
.