题目内容
15.已知数列{an}满足an+1-2an=2n(1)求证:{$\frac{{a}_{n}}{{2}^{n-1}}$}是等差数列;
(2)若a1=1,求an.
分析 (1)把已知等式两边同时除以2n,可得$\frac{{a}_{n+1}}{{2}^{n}}-\frac{{a}_{n}}{{2}^{n-1}}=1$,即数列{$\frac{{a}_{n}}{{2}^{n-1}}$}是公差为1的等差数列;
(2)由(1)求出数列{$\frac{{a}_{n}}{{2}^{n-1}}$}的通项公式,则an可求.
解答 (1)证明:由an+1-2an=2n,得
$\frac{{a}_{n+1}}{{2}^{n}}-\frac{{a}_{n}}{{2}^{n-1}}=1$,
∴数列{$\frac{{a}_{n}}{{2}^{n-1}}$}是公差为1的等差数列;
(2)解:由(1)知,数列{$\frac{{a}_{n}}{{2}^{n-1}}$}是公差为1的等差数列,
又a1=1,∴数列{$\frac{{a}_{n}}{{2}^{n-1}}$}的首项为$\frac{{a}_{1}}{{2}^{0}}=1$,
则$\frac{{a}_{n}}{{2}^{n-1}}$=1+1×(n-1)=n,
故${a}_{n}=n•{2}^{n-1}$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了等差数列通项公式的求法,是中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
20.以下数列是等比数列的为( )
| A. | 数列1,2,6,18,… | |
| B. | 常数列0,0,0,0,… | |
| C. | 在数列{an}中,已知$\frac{{a}_{2}}{{a}_{1}}$=2,$\frac{{a}_{3}}{{a}_{2}}$=2 | |
| D. | 在数列{an}中,$\frac{{a}_{n+1}}{{a}_{n}}$=q(其中q为非零常数,n∈N*) |
2.函数f(x)的导函数f′(x)的图象如图所示,则( )
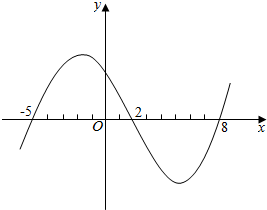

| A. | f(-2)>f(1) | B. | f(-2)<f(1) | ||
| C. | f(-2)=f(1) | D. | f(-2)与f(1)的大小不能确定 |
 ;
;