题目内容
8.函数f(x)=$\left\{\begin{array}{l}lnx({x>0})\\-\sqrt{-x}({x≤0})\end{array}$与g(x)=|x+a|+1的图象上存在关于y轴对称的点,则实数a的取值范围是( )| A. | R | B. | (-∞,-e] | C. | [e,+∞) | D. | ∅ |
分析 作出f(x)关于y轴对称的函数h(x)和g(x)的函数图象,根据h(x)与g(x)有交点得出a的范围.
解答 解:设y=h(x)与y=f(x)的图象关于y轴对称,
则h(x)=f(-x)=$\left\{\begin{array}{l}{ln(-x),x<0}\\{-\sqrt{x},x≥0}\end{array}\right.$,
作出y=h(x)与y=g(x)的函数图象如图所示:
∵f(x)与g(x)图象上存在关于y轴对称的点,
∴y=h(x)与y=g(x)的图象有交点,
∴-a≤-e,即a≥e.
故选C.
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
13.若椭圆的左焦点为F,上顶点为B,右顶点为A,当FB⊥AB时,其离心率为$\frac{{\sqrt{5}-1}}{2}$,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出“黄金双曲线”的离心率为( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{5}+1$ |
17.已知x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$,且b=-2x-y,当b取得最大值时,直线2x+y+b=0被圆(x-1)2+(y-2)2=25截得的弦长为( )
| A. | 10 | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
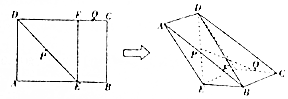 已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$.
已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A-EF-B大小为$\frac{2π}{3}$. 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.