题目内容
选修4-5:不等式选讲(本小题满分10分)
设函数 ,其中
,其中 。
。
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式 的解集为
的解集为 ,求a的值。
,求a的值。
(Ⅰ) 或
或 ;(II)
;(II) .
.
解析试题分析:(Ⅰ)当 时,
时, 可化为
可化为 。
。
由此可得  或
或 。
。
故不等式 的解集为
的解集为 或
或 。…………5分
。…………5分
( Ⅱ) 由 得
得 
此不等式化为不等式组 或
或
即  或
或
因为 ,所以不等式组的解集为
,所以不等式组的解集为
由题设可得 =
=  ,故
,故 …………10分
…………10分
考点:含绝对值不等式的解法。
点评:解含绝对值不等式的主要思想是分类讨论,通过分类讨论,去掉绝对值符号。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
在下列函数中,当x取正整数时,最小值为2的是
A.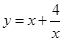 | B.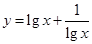 |
C.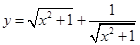 | D.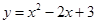 |
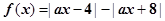 ,
,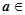 R
R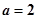 时,解不等式
时,解不等式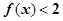 ;
;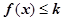 恒成立,求k的取值范围.
恒成立,求k的取值范围. 是实数,试解关于
是实数,试解关于 的不等式:
的不等式:
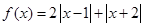 (1)求不等式
(1)求不等式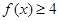 的解集;
的解集;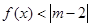 的解集是非空集合,求实数m的取值范围.
的解集是非空集合,求实数m的取值范围.
 且
且 ,求
,求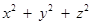 的最小值.
的最小值. 的不等式
的不等式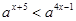 (
(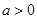 ,且
,且 ).
).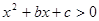 的解集为
的解集为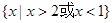
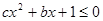 的解集.
的解集.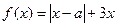 ,其中
,其中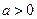 。
。 时,求不等式
时,求不等式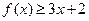 的解集;
的解集; 的解集为
的解集为 ,求a的值。
,求a的值。