题目内容
(本小题12分)已知不等式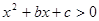 的解集为
的解集为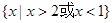
(1)求b和c的值; (2)求不等式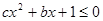 的解集.
的解集.
(1)b=-(2+1)=-3,c= ;(2)
;(2)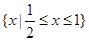 。
。
解析试题分析:(1)根据不等式的解集可知x=2,1是方程 的两根,从而根据韦达定理可求出b,c的值.
的两根,从而根据韦达定理可求出b,c的值.
(2)在(1)的基础上可知此不等式对应的二次函数是开口向上的抛物线,不等式的解应该取两零点之间的值.
(1)因为不等式 的解集为
的解集为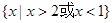 ,所以
,所以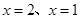 是方程
是方程 的两根,
的两根,
由韦达定理得:b=-(2+1)=-3,c= ................................6分
................................6分
(2)不等式化为: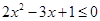 ,即
,即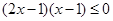 , ................................9分
, ................................9分 , ................................11分
, ................................11分
所以不等式的解集为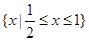 ................................12分
................................12分
考点:一元二次不等式的解法.
点评:解一元二次不等式要注意对应二次函数的开口方向,然后再根据不等式的符号,决定是取对应二次方程根的两边值还是中间值.

练习册系列答案
相关题目
已知 都是正实数,函数
都是正实数,函数 的图象过(0,1)点,则
的图象过(0,1)点,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
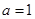 时,解不等式f(x)>3;
时,解不等式f(x)>3;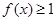 在区间(-∞,+∞)上恒成立,求实数a的取值范围.
在区间(-∞,+∞)上恒成立,求实数a的取值范围.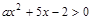 的解集是
的解集是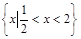 ,
,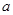 的值;
的值;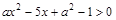 的解集.
的解集. ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求a的值。
,求a的值。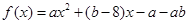 ,当
,当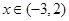 时,
时,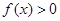 ;
;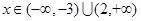 时,
时,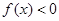 .
.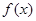 在
在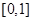 内的值域;
内的值域;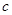 为何值时,
为何值时,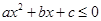 的解集为
的解集为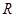 .
.
 时,求
时,求 的解集;
的解集; 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围. 是抛物线
是抛物线 的焦点,点
的焦点,点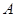 ,
, 在该抛物线上且位于
在该抛物线上且位于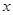 轴的两侧,
轴的两侧, (其中
(其中 为坐标原点),则
为坐标原点),则 与
与 面积之和的最小值是( )
面积之和的最小值是( )



 且
且
 时,求
时,求 的取值范围;
的取值范围; 时,求
时,求 的最小值.
的最小值.