题目内容
本小题满分12分)
解关于 的不等式
的不等式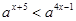 (
(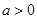 ,且
,且 ).
).
当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为
解析试题分析:当 时,函数
时,函数 在
在 上为减函数 . ……2分
上为减函数 . ……2分
由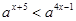 ,得
,得 ,即
,即 ……5分
……5分
当 时,函数
时,函数 在
在 上为增函数 . ……7分
上为增函数 . ……7分
由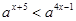 得
得 ,即
,即 . ……10分
. ……10分
综上,当 时,原不等式的解集为
时,原不等式的解集为 ;
;
当 时,原不等式的解集为
时,原不等式的解集为 . ……12分
. ……12分
考点:本小题主要考查指数函数的单调性和利用指数函数的单调性求解不等式,考查了学生分类讨论思想的应用和运算求解能力.
点评:分类讨论要做到不重不漏,而且最后一定要有综上所述,把各种情况一一列举出来,并写成集合点形式.

练习册系列答案
相关题目
设 ,则
,则 的最小值为( ).
的最小值为( ).
A. | B. | C. | D. |
若向量a=(x-1,2),b=(4,y)相互垂直,则9x+3y的最小值为( )
| A.12 | B.2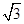 | C.3 | D.6 |
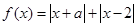
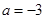 时,求不等式
时,求不等式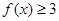 的解集;
的解集;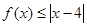 的解集包含
的解集包含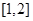 ,求
,求 的取值范围.
的取值范围.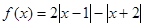
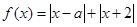 (a为常数,且a∈R).
(a为常数,且a∈R). ,其中
,其中 。
。 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求a的值。
,求a的值。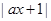 (a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.
(a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.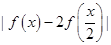 ≤k恒成立,求k的取值范围.
≤k恒成立,求k的取值范围.
 时,求
时,求 的解集;
的解集; 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.