题目内容
2．已知函数f（x）=x2+4x-5，分别求出它在下面区间上的值域．（1）x∈R；
（2）x∈[0，+∞]；
（3）x∈（-4，4）；
（4）x∈[0，2]．
分析 （1）根据开口方向，以及对称轴，确定单调性即可求出函数的值域；
（2）函数在[0，+∞）上单调递增函数，则在x=0处取最小值-5，即可求出函数的值域；
（3）函数在[0，2]上单调递增函数，则在x=0处取最小值-5，x=2处取得最大值7，即可求出函数的值域．
解答 解：（1）∵函数y=x2+4x-5=（x+2）2-9在（-∞，-2）上单调递减函数，在（-2，+∞）上单调递增函数
∴当x=-2时函数取最小值-9，
∴值域为[-9，+∞）；
（2）函数在[0，+∞）上单调递增函数，则在x=0处取最小值-5，
∴函数的值域为[-5，+∞）；
（3）函数y=x2+4x-5=（x+2）2-9在（-4，-2）上单调递减函数，在（-2，4）上单调递增函数
∴当x=-2时函数取最小值-9，
∵f（-4）=-5，f（4）=27
∴值域为[-9，27）；
（4）函数在[0，2]上单调递增函数，则在x=0处取最小值-5，x=2处取得最大值7
∴函数的值域为[-5，7]．
点评 本题主要考查了二次函数的值域问题，是高考中的热点问题，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=2sin（$\frac{π}{4}$x+φ）（|φ|＜$\frac{π}{2}$）的部分图象图象与x轴的交点分别为点P，Q（如图所示），图象上的点R的坐标为（4，$\sqrt{2}$）．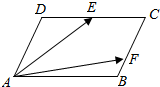
如图，平行四边形ABCD中，E为CD中点，F在线段BC上，且BC=3BF．已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$，则x的值为$\frac{6}{5}$．