题目内容
设函数f(x)＝Asin(ωx＋φ)(A＞0，ω＞0，|ω|≤π)的图象的最高点D的坐标为(2，
)，由最高点运动到最低相邻最低点F时，曲线与x轴相交于点E(6，0)，
(1)求A、ω、
的值，
(2)求函数y＝g(x)，使其图象与y＝f(x)图象关于直线x＝8对称．
答案：
解析：
解析：
|
解：(Ⅰ)最高点D(2， 由题意 综上，A＝ (Ⅱ)设P(x，y)为y＝g(x)上任一点，Q(xo，yo)是f(x)上关于x＝8对称点． y＝yo， 故y＝g(x)＝ |
)A＝
＝6－2＝4T＝16T＝
ω＝
f(x)＝sin(
)
，
，ω＝
＝8；y＝yo，xo＝16－x；又yo＝
＝
＝
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
相关题目
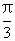)和g(x)＝btan(kx－
，且f(
)＝g(
)＝－
g(
)，g(x)＝btan(kx－
，已知f(
)＝g(
)＝－3g(
)(其中A＞0，ω＞0，－π＜
处取得最大值2，其图象与轴的相邻两个交点的距离为
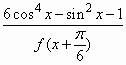的值域．