题目内容
当x∈[-2,2]时,ax<2(a>0且a≠1),则实数a范围是
- A.
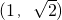
- B.

- C.
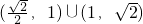
- D.
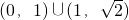
C
分析:由题,可根据a的取值范围分类讨论,分a>1时与0<a<1时两种情况讨论,根据函数的单调性确定出关于a的不等式,解出实数a的范围即可选出正确选项
解答:x∈[-2,2]时,ax<2(a>0且a≠1),
若a>1时,y=ax是一个增函数,则有a2<2,可得a< ,故有1<a<
,故有1<a< ,
,
若0<a<1,y=ax是一个减函数,则有a-2<2,可得a> ,故有
,故有 <a<1,
<a<1,
综上知a∈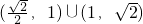
故选C
点评:本题考点是指数函数单调性的运用,考察了指数函数的单调性,一元二次不等式的解法,解题的关键是熟练掌握指数函数的单调性利用单调性确定出参数a所满足的不等式,从而解出a的取值范围.本题考察了判断推理的能力,计算题
分析:由题,可根据a的取值范围分类讨论,分a>1时与0<a<1时两种情况讨论,根据函数的单调性确定出关于a的不等式,解出实数a的范围即可选出正确选项
解答:x∈[-2,2]时,ax<2(a>0且a≠1),
若a>1时,y=ax是一个增函数,则有a2<2,可得a<
 ,故有1<a<
,故有1<a< ,
,若0<a<1,y=ax是一个减函数,则有a-2<2,可得a>
 ,故有
,故有 <a<1,
<a<1,综上知a∈
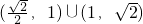
故选C
点评:本题考点是指数函数单调性的运用,考察了指数函数的单调性,一元二次不等式的解法,解题的关键是熟练掌握指数函数的单调性利用单调性确定出参数a所满足的不等式,从而解出a的取值范围.本题考察了判断推理的能力,计算题

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目