Question

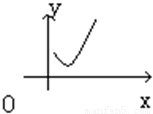
下列四个函数中，图象为如图所示的只可能是（　　）

• A、y=2x+1nx
• B、y=2x-1nx
• C、y=-2x+1nx
• D、y=-2x-1nx

Answer 1

分析：先求出所给函数的导数，再结合导数的符号，判断函数的单调性，然后利用函数的单调性进行求解．

解答：解：在y=2x+1nx中，y′=2+

1

x

＞0，∴y=2x+1nx是增函数，∴A不成立；
在y=2x-1nx中，y′=2-

1

x

，当0＜x＜

1

2

时，y′=2-

1

x

＜0，当x＞

1

2

时，y′=2-

1

x

＞0．∴y=2x-1nx的增区间是[

1

2

，+∞)，减区间是（0，

1

2

]，∴B成立；
在y=-2x+1nx中，y′=-2+

1

x

．当0＜x＜

1

2

时，y′=-2+

1

x

＞0，当x＞

1

2

时，y′=-2+

1

x

＜0．∴y=-2x+1nx的减区间是[

1

2

，+∞)，增区间是（0，

1

2

]，∴C不成立；
在y=-2x-1nx中，y′=-2-

1

x

＜0，∴y=-2x-1nx是减函数，∴D不成立．
故选B．

点评：本题考查对数函数的图象和性质，解题时要注意导数的合理运用．