题目内容
下列四个函数中，图象既关于直线x=
π对称，又关于点(
，0)对称的是（ ）
| 5 |
| 12 |
| π |
| 6 |
分析：求出各个函数的图象的对称轴，若图象不关于直线x=
对称，即可排除此选项．若图象关于直线x=
对称，
再令x=
，看函数值是否等于零，从而得出结论．
| 5π |
| 12 |
| 5π |
| 12 |
再令x=
| π |
| 6 |
解答：解：由于函数y=sin(2x-
)，令2x-
=kπ+
，可得它的对称轴为 x=
+
，k∈z，故关于直线x=
对称．
再令x=
可得 y=sin(2x-
)=0，故图象也关于点（
，0）对称，故A满足条件．
由于函数y=sin(2x+
)，令2x+
=kπ+
可得它的对称轴为 x=
+
，k∈z，故不关于直线x=
对称，
故B不满足条件．
由于函数y=sin(4x+
)，令4x+
=kπ+
，可得它的对称轴为 x=
+
，k∈z，故不关于直线x=
对称，
故C不满足条件．
由于函数 y=sin(4x-
)，令4x-
=kπ+
，可得它的对称轴为 x=
+
，k∈z，关于直线x=
对称．
再令x=
可得 4x-
=
，y=sin(4x-
)=1，可得它的图象不关于点（
，0）对称，故D不满足条件．
故选A．
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 12 |
| 5π |
| 12 |
再令x=
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
由于函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
故B不满足条件．
由于函数y=sin(4x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| kπ |
| 4 |
| π |
| 12 |
| 5π |
| 12 |
故C不满足条件．
由于函数 y=sin(4x-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| kπ |
| 4 |
| π |
| 6 |
| 5π |
| 12 |
再令x=
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
故选A．
点评：本题主要考查正弦函数的图象的对称轴和对称中心，属于中档题．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
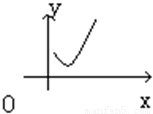
下列四个函数中，图象为如图所示的只可能是（ ）| A、y=2x+1nx | B、y=2x-1nx | C、y=-2x+1nx | D、y=-2x-1nx |
（2007•上海）下列四个函数中，图象如图所示的只能是（ ）
下列四个函数中，图象如图1所示的只能是（ ）