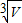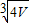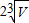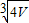题目内容
设底部为三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为( )
A.
| B.
| C.
| D.2
|
设底边边长为a,高为h,则V=Sh=
a2×h,
∴h=
,
表面积为S=3ah+
a2
=
+
a2
=
+
+
a2
≥3
=定值,
等号成立的条件
=
a2,即a=
,
故选C.
| ||
| 4 |
∴h=
4
| ||
| 3a2 |
表面积为S=3ah+
| ||
| 2 |
=
4
| ||
| a |
| ||
| 2 |
=
2
| ||
| a |
2
| ||
| a |
| ||
| 2 |
≥3
| 3 |
| ||||||||||||
等号成立的条件
2
| ||
| a |
| ||
| 2 |
| 3 | 4V |
故选C.

练习册系列答案
相关题目
设底部为三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为( )
|
| A. |
| B. |
| C. |
| D. |
|