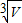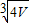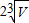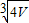Question

设底部为三角形的直棱柱的体积为V，那么其表面积最小时，底面边长为（　　）

A．

B．

C．

D．

Answer 1

考点：

平均值不等式；棱柱、棱锥、棱台的侧面积和表面积；棱柱、棱锥、棱台的体积．

专题：

计算题．

分析：

设底边边长为a，高为h，利用体积公式V=Sh= a²×h，得出 h=，再根据表面积公式得S=+a²，最后利用基本不等式求出它的最大值及等号成立的条件即得．

解答：

解：设底边边长为a，高为h，则V=Sh= a²×h，

∴h=，

表面积为S=3ah+a²=+a²=++a²≥3=定值，

等号成立的条件，即a=，

故选C．

点评：

本小题主要考查棱柱、棱锥、棱台、棱柱、棱锥、棱台的侧面积和表面积、基本不等式等基础知识，考查运算求解能力，考查转化思想．属于基础题．