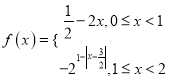题目内容
【题目】在锐角三角形![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】解:(Ⅰ)因为![]() ,
,
所以![]() , ……………………………………………… 2分
, ……………………………………………… 2分
因为![]() ,所以
,所以![]() . …………………………………………………3分
. …………………………………………………3分
又![]() 为锐角,则
为锐角,则![]() . …………………………………………… 5分
. …………………………………………… 5分
(Ⅱ)由(Ⅰ)可知,![]() .因为
.因为![]() ,
,
根据余弦定理,得![]() ,………………………………………7分
,………………………………………7分
整理,得![]() .
.
由已知![]() ,则
,则![]() .
.
又![]() ,可得
,可得![]() ,
,![]() . ……………………………………… 9分
. ……………………………………… 9分
于是![]() , ………………………… 11分
, ………………………… 11分
所以![]() . …………… 13分
. …………… 13分
【解析】试题分析:(1)由正弦定理可得![]() ,即
,即![]() ,则角
,则角![]() 可求;
可求;
(2))由(1)知,![]() ,由余弦定理可得
,由余弦定理可得![]() ,进而求得
,进而求得![]() 则
则![]() 的值可求
的值可求
试题解析:(1)因为![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() ,又
,又![]() 为锐角,则
为锐角,则![]() .
.
(2)由(1)知,![]() ,因为
,因为![]() ,根据余弦定理得:
,根据余弦定理得:![]() ,整理,得
,整理,得![]() ,由已知
,由已知![]() ,则
,则![]() ,又
,又![]() ,可得
,可得![]() ,于是
,于是![]() ,
,
所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目