题目内容

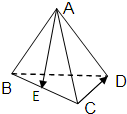
正四面体ABCD中，E、F分别是棱BC、AD的中点，则直线DE与平面BCF所成角的正弦值为（　　）
A．
2
2
3
B．
3
3
C．
6
3
D．
2
2
连接EF，由BF=CF，BD=CD
可得FE⊥BC，DE⊥BC
∴∠FED是线面所成角
设棱长a，CD=a，ED=BF=CF=
3
2
a
三角形BCF是等腰三角形，则EF=
2
2
a
由余弦定理，cos∠FED=
6
3

则SIN∠FED=
3
3

故选B
练习册系列答案
相关题目
在的棱长为1的正四面体ABCD中，E是BC的中点，则
AE
•
CD
=（　　）
A、0
B、
1
2
C、-
1
2
D、-
1
4
精英家教网在棱长为1的正四面体ABCD中，E是BC的中点，则
AE
•
CD
=
 
．
4、求证：正四面体ABCD中相对的两棱（即异面的两棱）互相垂直．
某同学使用类比推理得到如下结论：
（1）同一平面内，三条不同的直线a，b，c，若a⊥c，b⊥c，则a∥b，类比出：空间中，三条不同的直线a，b，c，若a⊥c，b⊥c，则a∥b；
（2）a，b∈R，a-b＞0则a＞b，类比出：a，b∈C，a-b＞0则a＞b；
（3）以点（0，0）为圆心，r为半径的圆的方程是x2+y2=r2，类比出：以点（0，0，0）为球心，r为半径的球的方程是x2+y2+z2=r2；
（4）正三角形ABC中，M是BC的中点，O是△ABC外接圆的圆心，则
AO
OM
=2，类比出：在正四面体ABCD中，若M是△BCD的三边中线的交点，O为四面体ABCD外接球的球心，则
AO
OM
=3．
其中类比的结论正确的个数是（　　）
在正四面体ABCD中，E、F分别为棱AD、BC的中点，连接AF、CE，则异面直线AF和CE所成角的正弦值为（　　）
A、
1
3
B、
2
3
C、
2
4
D、
5
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网