题目内容
已知向量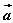 =(
=( cosx,0),
cosx,0),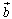 =(0,sinx),记函数f(x)=
=(0,sinx),记函数f(x)=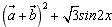 。
。
(1)求函数f(x)的最小值及取最小值时x的集合;
(2)若将函数f(x)的图象按向量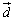 平移后,得到的图象关于坐标原点成中心对称,且在[0,
平移后,得到的图象关于坐标原点成中心对称,且在[0,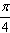 ]上单调递减,求长度最小的
]上单调递减,求长度最小的 。
。
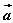 =(
=( cosx,0),
cosx,0),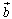 =(0,sinx),记函数f(x)=
=(0,sinx),记函数f(x)=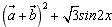 。
。(1)求函数f(x)的最小值及取最小值时x的集合;
(2)若将函数f(x)的图象按向量
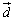 平移后,得到的图象关于坐标原点成中心对称,且在[0,
平移后,得到的图象关于坐标原点成中心对称,且在[0,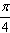 ]上单调递减,求长度最小的
]上单调递减,求长度最小的 。
。解:(1)∵


∴当且仅当 ,即
,即 (k∈Z)时
(k∈Z)时
f(x)min=0
此时x的集合是 ;
;
(2)设f(x)的图象按向量 平移后对应的函数为g(x)
平移后对应的函数为g(x)
则
∵g(x)的图象关于坐标原点成中心对称
∴ ,且
,且
解得 (k∈Z),且
(k∈Z),且
 时,
时, 在
在 上单调递增,不合题意,舍去;
上单调递增,不合题意,舍去;
 时,
时, 在
在 上单调递减,符合题意
上单调递减,符合题意
∴ (k∈Z)
(k∈Z)
∴长度最小的 。
。



∴当且仅当
 ,即
,即 (k∈Z)时
(k∈Z)时f(x)min=0
此时x的集合是
 ;
;(2)设f(x)的图象按向量
 平移后对应的函数为g(x)
平移后对应的函数为g(x)则

∵g(x)的图象关于坐标原点成中心对称
∴
 ,且
,且
解得
 (k∈Z),且
(k∈Z),且
 时,
时, 在
在 上单调递增,不合题意,舍去;
上单调递增,不合题意,舍去; 时,
时, 在
在 上单调递减,符合题意
上单调递减,符合题意∴
 (k∈Z)
(k∈Z)∴长度最小的
 。
。
练习册系列答案
相关题目