题目内容
6. 如图,半圆的直径AB=2,D是半圆弧上一点,DC与半圆相切,且DC=2,设∠BAD=α.
如图,半圆的直径AB=2,D是半圆弧上一点,DC与半圆相切,且DC=2,设∠BAD=α.(1)用α表示四边形ABCD的面积S;
(2)当α为何值时,四边形面积S最大?面积的最大值是多少?
分析 (1)记圆心为O,连结BD、OD,利用三角形面积公式及二倍角公式计算即可;
(2)S=$\sqrt{2}$sin(2α-$\frac{π}{4}$)+1取最大值等价于y=sin(2α-$\frac{π}{4}$)取最大值,计算即可.
解答 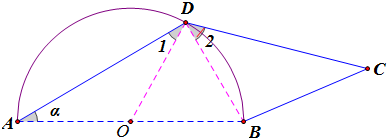 解:(1)记圆心为O,连结BD、OD,
解:(1)记圆心为O,连结BD、OD,
由题易知:∠1=∠2=α,BD=ABsinα=2sinα,
AD=ABcosα=2cosα,
则S=$\frac{1}{2}$AD•BD+$\frac{1}{2}$DC•DBsin∠2
=$\frac{1}{2}$AD•BD+$\frac{1}{2}$DC•DBsinα
=$\frac{1}{2}$•2cosα•2sinα+$\frac{1}{2}$•2•2sinα•sinα
=2sinαcosα+2sin2α
=sin2α+1-cos2α
=$\sqrt{2}$sin(2α-$\frac{π}{4}$)+1;
(2)∵S=$\sqrt{2}$sin(2α-$\frac{π}{4}$)+1,
∴当2α-$\frac{π}{4}$=$\frac{π}{2}$+2kπ时S最大,
∴当α=$\frac{3}{8}$π时S最大,面积的最大值为:$\sqrt{2}+1$.
点评 本题是一道三角函数的应用题,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.如图所示,程序框图的功能是( )


| A. | 求{$\frac{1}{n}$}前10项和 | B. | 求{$\frac{1}{2n}$}前10项和 | C. | 求{$\frac{1}{n}$}前11项和 | D. | 求{$\frac{1}{2n}$}前11项和 |
17.根据如下样本数据
得到的回归方程为$\stackrel{∧}{y}$=bx+a.若a=7.9,则b的值为-1.4.
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 |
14.将6名留学归国人员分配到济南、青岛两地工作.若济南至少安排2 人,青岛至少安排3人,则不同的安排方法数为( )
| A. | 120 | B. | 150 | C. | 35 | D. | 55 |
16.设复数z=-1-i(i为虚数单位),则$\frac{2-\overline{z}}{z}$对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.