题目内容
【题目】(1)在圆中有这样的结论:对圆![]() 上任意一点
上任意一点![]() ,设
,设![]() 、
、![]() 是圆和
是圆和![]() 轴的两交点,且直线
轴的两交点,且直线![]() 和
和![]() 的斜率都存在,则它们的斜率之积为定值-1.试将该结论类比到椭圆
的斜率都存在,则它们的斜率之积为定值-1.试将该结论类比到椭圆![]() ,并给出证明.
,并给出证明.
(2)已知椭圆![]() ,
,![]() ,
,![]() ,设直线
,设直线![]() 与椭圆
与椭圆![]() 交于不同于
交于不同于![]() 、
、![]() 的两点
的两点![]() 、
、![]() ,记直线
,记直线![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() .
.
(ⅰ)若直线![]() 过定点
过定点![]() ,则
,则![]() 是否为定值.若是,请证明;若不是,请说明理由.
是否为定值.若是,请证明;若不是,请说明理由.
(ⅱ)若![]() ,求所有整数
,求所有整数![]() ,使得直线
,使得直线![]() 变化时,总有
变化时,总有![]() .
.
【答案】(1)对椭圆![]() 上任意一点
上任意一点![]() ,设
,设![]() 、
、![]() 是椭圆和
是椭圆和![]() 轴的两交点,且直线
轴的两交点,且直线![]() 和
和![]() 的斜率都存在,则它们的斜率之积为定值
的斜率都存在,则它们的斜率之积为定值![]() ;证明见解析(2)(ⅰ)是定值;证明见解析(ⅱ)
;证明见解析(2)(ⅰ)是定值;证明见解析(ⅱ)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)利用类比推理得:设![]() 、
、![]() 是椭圆和
是椭圆和![]() 轴的两交点,
轴的两交点,![]() 为椭圆上任一点,且直线
为椭圆上任一点,且直线![]() 和
和![]() 的斜率都存在,则它们的斜率之积为定值,若设
的斜率都存在,则它们的斜率之积为定值,若设![]() ,
,![]() ,
,![]() ,然后利用斜率公式可证出结论;
,然后利用斜率公式可证出结论;
(2)由于![]() ,
,![]() 恰好是椭圆与
恰好是椭圆与![]() 轴的交点,
轴的交点,![]() 、
、![]() 是椭圆上任意两点,所以在此题的求解中利用一元二次方程的根与系数的关系,再结合(1)中得到的结论可得答案.
是椭圆上任意两点,所以在此题的求解中利用一元二次方程的根与系数的关系,再结合(1)中得到的结论可得答案.
(1)对椭圆![]() 上任意一点
上任意一点![]() ,设
,设![]() 、
、![]() 是椭圆和
是椭圆和![]() 轴的两交点,且直线
轴的两交点,且直线![]() 和
和![]() 的斜率都存在,则它们的斜率之积为定值
的斜率都存在,则它们的斜率之积为定值![]() ,
,
证明:设![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,
则 ,
,
(2)(ⅰ)![]() ,设
,设![]() ,
,![]() ,
,
联立直线与椭圆方程,得![]() ,则
,则 (*)
(*)

将(*)代入,得![]() 为定值.
为定值.
(ⅱ)当时,直线![]() 过定点
过定点![]() ,其中
,其中![]() ,
,
联立直线与椭圆方程,得![]() ,由
,由![]() ,可得
,可得![]() 或
或![]() ,
,
由(1)得![]() ,从而
,从而![]() ,
,
![]() ,
,
![]() 符合题意的整数
符合题意的整数![]() 为
为![]() ,
,![]() ,
,![]() ,
,![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: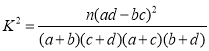 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
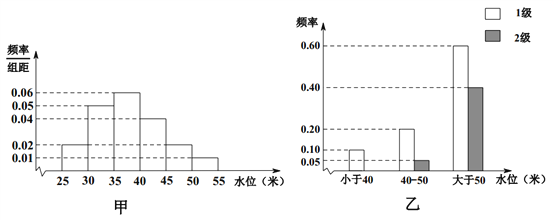
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.