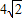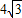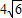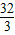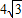题目内容
在△ABC中,a=80,b=100,A=30°,则B的解的个数是
- A.0
- B.1
- C.2
- D.无法确定
C
分析:根据正弦定理得到sinB的值,然后因为B为三角形中的角即B∈(0,π),利用正弦函数的图象得到B满足条件的个数即可
解答:因为a=80,b=100,A=30°,
根据正弦定理得: =
= ,
,
代入得到sinB= ,由于B∈(0,π),
,由于B∈(0,π),
所以B=arcsin 或B=π-arcsin
或B=π-arcsin
故选C
点评:考查学生灵活运用正弦定理解决实际问题的能力,以及会根据三角函数值求出满足的角.
分析:根据正弦定理得到sinB的值,然后因为B为三角形中的角即B∈(0,π),利用正弦函数的图象得到B满足条件的个数即可
解答:因为a=80,b=100,A=30°,
根据正弦定理得:
 =
= ,
,代入得到sinB=
 ,由于B∈(0,π),
,由于B∈(0,π),所以B=arcsin
 或B=π-arcsin
或B=π-arcsin
故选C
点评:考查学生灵活运用正弦定理解决实际问题的能力,以及会根据三角函数值求出满足的角.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
在△ABC中,a=8,B=60°,C=75°,则b=( )
A、4
| ||
B、4
| ||
C、4
| ||
D、
|