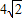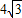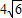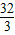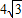Question

在△ABC中，a=8，b=7，B=60°．求c及S_△ABC．

Answer 1

分析：由a，b及cosB的值，利用余弦定理求出c的值，再由a，c及sinB的值，利用三角形的面积公式即可求出三角形ABC的面积．

解答：解：∵在△ABC中，a=8，b=7，B=60°，
∴由余弦定理得：b²=a²+c²-2accosB，即49=64+c²-8c，
解得：c=3或c=5，
则S_△ABC=

1

2

acsinB=6

3

或10

3

．

点评：此题考查了余弦定理，以及三角形的面积公式，熟练掌握余弦定理是解本题的关键．