题目内容
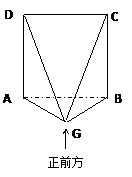
如图，四棱锥G—ABCD中，ABCD是正方形，且边长为2a，面ABCD⊥面ABG，AG=BG。
（1）画出四棱锥G—ABCD的三视图；
 |
（2）在四棱锥G—ABCD中，过点B作平面
AGC的垂线，若垂足H在CG上，
求证：面AGD⊥面BGC
（3）在（2）的条件下，求三棱锥D—ACG的体积
及其外接球的表面积。
解析:
（1）三视图（见右图）
（2）ABCD是正方形 ∴ BC⊥AB
∵面ABCD⊥面ABG ∴ BC⊥面ABG
∵AG
面ABG ∴ BC⊥AG
又 BH⊥面AGC ∴ BH⊥AG
∵ BC
BH=B ∴ AG⊥面AGD
∴面AGD⊥面BGC
（3）由（2）知 AG⊥面BGC ∴AG⊥BG 又AG=BG
∴ △ABG是等腰Rt△，取AB中点E，
连结GE，则GE⊥AB
∴ GE⊥面ABCD
∴ 
又
∴ 取AC中点M，则 
因此：
即点M是三棱锥D—ACG的外接球的球心，
半径为
∴ 
练习册系列答案
阅读快车系列答案
相关题目
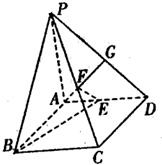如图在四棱锥P-ABCD中，底ABCD是矩形，PA⊥面ABCD，AP=AB=2，BC=2
（2013•自贡一模）如图，四棱锥P-ABCD的底ABCD是矩形，PA⊥平面ABCD，AD=2，AB=1，E，F分别是AB，BC的中点N在轴上．
如图，四棱锥A-BCDE中，△ABC是正三角形，四边形BCDE是矩形，且平面ABC⊥平面BCDE，AB=2，AD=4．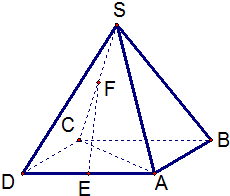
如图，四棱锥S-ABCD中，底面ABCD为平行四边形，点E、F、G分别是棱AD、SC、BC的中点．
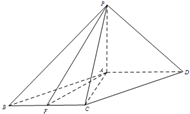（2012•顺义区一模）如图：四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB=90°，PA⊥平面ABCD，PA=BC=1，