题目内容
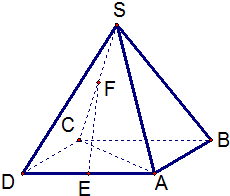 如图,四棱锥S-ABCD中,底面ABCD为平行四边形,点E、F、G分别是棱AD、SC、BC的中点.
如图,四棱锥S-ABCD中,底面ABCD为平行四边形,点E、F、G分别是棱AD、SC、BC的中点.(1)求证:EF∥平面SAB;
(2)若SB=SC=AB=AC,求证:平面SBC⊥平面SAG;
(3)若SA=SB=SC=AB=AC=2,BC=2
| 2 |
分析:(1)取SB的中点为H,连接FH、AH,kd FH∥BC,并且FH=
BC,即可得到FH∥EA,并且FH=EA,即四边形AHFE为平行四边形,进而得到FE∥AH,再根据线面平行的判定定理即可证明线面平行.
(2)连接AG,SG,由AB=AC,并且G为BC的中点,可得AG⊥BC,同理可得:SG⊥BC,再结合线面垂直与面垂直的判定定理即可证明面面垂直.
(3)由题意可得:VD-SAC=VS-ACD,即可得到VS-ACD=VS-ABC.根据线段的长度关系并且在△ABC中结合勾股定理可得:AC⊥AB,并且AG=
,同理可得:SG=
,在△AGS中根据勾股定理可得SG⊥AG,进一步得到SG⊥平面ABC,进而求出三棱锥的体积.
| 1 |
| 2 |
(2)连接AG,SG,由AB=AC,并且G为BC的中点,可得AG⊥BC,同理可得:SG⊥BC,再结合线面垂直与面垂直的判定定理即可证明面面垂直.
(3)由题意可得:VD-SAC=VS-ACD,即可得到VS-ACD=VS-ABC.根据线段的长度关系并且在△ABC中结合勾股定理可得:AC⊥AB,并且AG=
| 2 |
| 2 |
解答:解:(1)证明:取SB的中点为H,连接FH、AH,

因为F、H分别为SC、SB的中点,
所以FH∥BC,并且FH=
BC,
又因为E为AD的中点,
所以EA∥BC,并且EA=
BC,
所以FH∥EA,并且FH=EA,
所以四边形AHFE为平行四边形,
所以FE∥AH,
又因为AH?平面ABS,EF?平面ABS,
所以EF∥平面SAB.
(2)证明:连接AG,SG,
因为AB=AC,并且G为BC的中点,
所以AG⊥BC,
同理可得:SG⊥BC,
因为AG∩SG=G,AG?平面SAG,SG?平面SAG,
所以BC⊥平面SAG,
又因为BC?平面SBC,
所以平面SBC⊥平面SAG.
(3)由题意可得:VD-SAC=VS-ACD,
因为在四棱锥S-ABCD中,并且底面ABCD为平行四边形,
所以VS-ACD=VS-ABC.
因为AB=AC=2,BC=2
,
所以在△ABC中,根据勾股定理可得:AC⊥AB,并且AG=
,
同理可得:SG=
,
因为SA=2,
所以在△AGS中,根据勾股定理可得SG⊥AG.
又由(2)可得SG⊥BC,
所以SG⊥平面ABC.
所以VS-ACD =VS-ABC=
•S△ABC•SG=
×
×2×2×
=
,
所以三棱锥D-SAC的体积为
.

因为F、H分别为SC、SB的中点,
所以FH∥BC,并且FH=
| 1 |
| 2 |
又因为E为AD的中点,
所以EA∥BC,并且EA=
| 1 |
| 2 |
所以FH∥EA,并且FH=EA,
所以四边形AHFE为平行四边形,
所以FE∥AH,
又因为AH?平面ABS,EF?平面ABS,
所以EF∥平面SAB.
(2)证明:连接AG,SG,
因为AB=AC,并且G为BC的中点,
所以AG⊥BC,
同理可得:SG⊥BC,
因为AG∩SG=G,AG?平面SAG,SG?平面SAG,
所以BC⊥平面SAG,
又因为BC?平面SBC,
所以平面SBC⊥平面SAG.
(3)由题意可得:VD-SAC=VS-ACD,
因为在四棱锥S-ABCD中,并且底面ABCD为平行四边形,
所以VS-ACD=VS-ABC.
因为AB=AC=2,BC=2
| 2 |
所以在△ABC中,根据勾股定理可得:AC⊥AB,并且AG=
| 2 |
同理可得:SG=
| 2 |
因为SA=2,
所以在△AGS中,根据勾股定理可得SG⊥AG.
又由(2)可得SG⊥BC,
所以SG⊥平面ABC.
所以VS-ACD =VS-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
2
| ||
| 3 |
所以三棱锥D-SAC的体积为
2
| ||
| 3 |
点评:本题主要考查线线平行,线面平行与垂直的判定定理,以及面面垂直的判定定理,解决此类问题的关键是熟练记忆有关的判定定理、性质定理,以及熟悉几何体的结构特征.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.