题目内容
6.直三棱柱ABC-A1B1C1中,∠A1B1C1=90°,且AB=BC=BB1,E,F分别是AB,CC1的中点,那么直线A1C与EF所成的角的余弦值为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
分析 以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,利用向量法能求出直线A1C与EF所成的角的余弦值.
解答  解:以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,
解:以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,
设AB=BC=BB1=2,则E(1,0,0),F(0,2,1),
A1(2,0,2),C(0,2,0),
$\overrightarrow{{A}_{1}C}$=(-2,2,-2),$\overrightarrow{EF}$=(-1,2,1),
设直线A1C与EF所成的角为θ,
则cosθ=|cos<$\overrightarrow{{A}_{1}C}$,$\overrightarrow{EF}$>|=|$\frac{\overrightarrow{{A}_{1}C}•\overrightarrow{EF}}{|\overrightarrow{{A}_{1}C}|•|\overrightarrow{EF}|}$|=|$\frac{2+4-2}{\sqrt{12}•\sqrt{6}}$|=$\frac{\sqrt{2}}{3}$.
∴直线A1C与EF所成的角的余弦值为$\frac{\sqrt{2}}{3}$.
故选:D.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
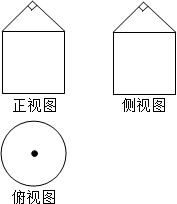
1.如图是一个三棱锥的三视图,俯视图是一个斜边长为2的直角三角形,设它的外接球的表面积为S,则( )
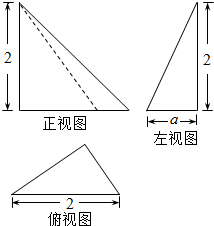

| A. | S是定值,S=8π | B. | S不是定值,有最小值Smin=8π | ||
| C. | S不是定值,有最大值Smax=8π | D. | S不是定值,与a的大小有关 |
18.某四棱锥的三视图如图所示,则该四棱锥的体积是( )
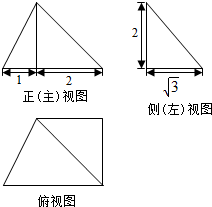

| A. | $5\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{{5\sqrt{3}}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
15.已知双曲线C:$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1的左右焦点分别为F1、F2,若双曲线C的右支上存在一点P,使得($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,O为坐标原点,且|$\overrightarrow{P{F}_{1}}$|=λ|$\overrightarrow{P{F}_{2}}$|,则实数λ等于( )
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
16.方程x-lg$\frac{1}{x}$-3=0的解所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
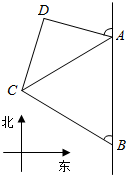 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3$\sqrt{2}$海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离多少海里?