题目内容
下列函数中,既是偶函数又在区间 上单调递增的函数为( )
上单调递增的函数为( )
A.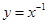 | B. | C. | D. |
C
解析试题分析:A是奇函数,B既不是奇函数,也不是偶函数,所以,A、B都排除;D是二次函数,函数图象的开口向下,在 单调递减,不符合,只有C符合.
单调递减,不符合,只有C符合.
考点:1、函数的奇偶性;2、函数的单调性以及基本初等函数的图象.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
设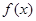 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,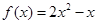 ,则
,则 ( )
( )
A. | B. | C. | D. |
有下列四个命题:
①对于 ,函数
,函数 满足
满足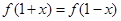 ,则函数
,则函数 的最小正周期为2;
的最小正周期为2;
②所有指数函数的图象都经过点 ;
;
③若实数 满足
满足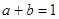 ,则
,则 的最小值为9;
的最小值为9;
④已知两个非零向量 ,
,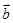 ,则“
,则“
 ”是“
”是“ ”的充要条件.
”的充要条件.
其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
函数 的零点所在的一个区间是 ( )
的零点所在的一个区间是 ( )
A. | B. | C. | D. |
定义在 上的奇函数
上的奇函数 ,满足
,满足 ,
, ,则函数
,则函数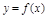 在区间
在区间 内零点个数的情况为( )
内零点个数的情况为( )
A. 个 个 | B. 个 个 | C. 个 个 | D.至少 个 个 |
 ,若存在实数
,若存在实数 、
、 、
、 、
、 ,满足
,满足
 ,其中
,其中 ,则
,则 的取值范围是 .
的取值范围是 . 的反函数
的反函数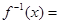 ________________.
________________.  满足
满足 ,则称
,则称 ; ②
; ② ;
;
 是
是 的内角).
的内角).



 ,如果存在区间
,如果存在区间 ,同时满足下列条件:①
,同时满足下列条件:① 在
在 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )


