题目内容
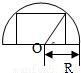
 在圆心为O、半径为常数R的半圆板内画内接矩形(如图),当矩形的长和宽各取多少时,矩形的面积最大?求出这个最大面积.
在圆心为O、半径为常数R的半圆板内画内接矩形(如图),当矩形的长和宽各取多少时,矩形的面积最大?求出这个最大面积.
分析:如图用圆的半径R与图中所示的角(可设出)表示出来,把此矩形的面积表示出来,再用三角函数的相关的公式化简,最后用三角函数的有界性判断最大值在什么情况下取到,求出矩形的最大面积以及矩形的长与宽的大小.
解答:解:设矩形在半圆板直径上的一边长为2x,α角如图所示,
则x=Rcosα,另一边的长为Rsinα,矩形面积S为
S=2R2sinαcosα.
=R2sin2α
当2α=
即α=
时,也即长为2Rcos
=
R,
宽为Rsin
=
R时,矩形面积最大
最大面积是R2
则x=Rcosα,另一边的长为Rsinα,矩形面积S为
S=2R2sinαcosα.
=R2sin2α
当2α=
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
宽为Rsin
| π |
| 4 |
| ||
| 2 |
最大面积是R2
点评:本题考查用三角函数解决实际问题的最值,这是三角函数的一个重要的运用,请仔细体会本题中函数关系的建立过程.

练习册系列答案
相关题目
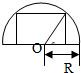
 在圆心为O、半径为常数R的半圆板内画内接矩形(如图),当矩形的长和宽各取多少时,矩形的面积最大?求出这个最大面积.
在圆心为O、半径为常数R的半圆板内画内接矩形(如图),当矩形的长和宽各取多少时,矩形的面积最大?求出这个最大面积.