题目内容
x1与x2分别是实系数方程ax2+bx+c=0和-ax2+bx+c=0的一个根,且x1≠x2,x1≠0,x2≠0.求证:方程| a | 2 |
分析:先由x1与x2分别是实系数方程ax2+bx+c=0和-ax2+bx+c=0的一个根,得到关于x1与x2的两个等式,再设f(x)=
x2+bx+c,利用条件推出f(x1)f(x2)<0,即可说明方程
x2+bx+c=0有一个根介于x1和x2之间.
| a |
| 2 |
| a |
| 2 |
解答:证明:由于x1与x2分别是方程ax2+bx+c=0和-ax2+bx+c=0的根,
所以有
设f(x)=
x2+bx+c,
则f(x1)=
x12+bx1+c=-
x12,
f(x2)=
x22+bx2+c=
x22,
∴f(x1)f(x2)=-
a2x12x22
由于x1≠x2,x1≠0,x2≠0,
所以f(x1)f(x2)<0,
因此方程
x2+bx+c=0有一个根介于x1和x2之间.
所以有
|
设f(x)=
| a |
| 2 |
则f(x1)=
| a |
| 2 |
| a |
| 2 |
f(x2)=
| a |
| 2 |
| 3a |
| 2 |
∴f(x1)f(x2)=-
| 3 |
| 4 |
由于x1≠x2,x1≠0,x2≠0,
所以f(x1)f(x2)<0,
因此方程
| a |
| 2 |
点评:本题考查一元二次方程根的分布问题.在解题过程中用到了零点存在性定理,若想说函数在某个区间上有零点,只要区间两端点值异号即可.

练习册系列答案
相关题目
 x2+bx+c=0有仅有一根介于x1和x2之间。
x2+bx+c=0有仅有一根介于x1和x2之间。 x2+bx+c=0有一个根介于x1和x2之间.
x2+bx+c=0有一个根介于x1和x2之间.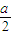 x2+bx+c=0有一个根介于x1和x2之间.
x2+bx+c=0有一个根介于x1和x2之间.