题目内容
已知![]() 在
在![]() 时取得极值,且
时取得极值,且![]() .
.
1.试求常数a、b、c的值;
2.试判断![]() 是函数的极小值还是极大值,并说明理由.
是函数的极小值还是极大值,并说明理由.
1. ![]() .
.
![]() 是函数
是函数![]() 的极值点,
的极值点,
∴![]() 是方程
是方程![]() ,即
,即![]() 的两根,
的两根,
由根与系数的关系,得
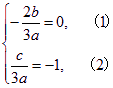
又![]() ,∴
,∴![]() , (3)
, (3)
由(1)、(2)、(3)解得![]() .
.
2.![]() ,∴
,∴![]()
当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
∴函数![]() 在
在![]() 和
和![]() 上是增函数,在(-1,1)上是减函数.
上是增函数,在(-1,1)上是减函数.
∴当![]() 时,函数取得极大值
时,函数取得极大值![]() ,
,
当![]() 时,函数取得极小值
时,函数取得极小值![]() .
.
解析:
考察函数![]() 是实数域上的可导函数,可先求导确定可能的极值点,再通过极值点与导数的关系,即极值点必为
是实数域上的可导函数,可先求导确定可能的极值点,再通过极值点与导数的关系,即极值点必为![]() 的根建立起由极值点
的根建立起由极值点![]() 所确定的相关等式,运用待定系数法求出参数a、b、c的值.
所确定的相关等式,运用待定系数法求出参数a、b、c的值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
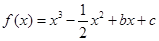
 的图象有与
的图象有与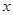 轴平行的切线,求
轴平行的切线,求 的取值范围;
的取值范围;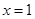 时取得极值,且
时取得极值,且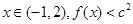 恒成立,求
恒成立,求 的取值范围.
的取值范围. 。
。 的图象有与
的图象有与 轴平行的切线,求
轴平行的切线,求 的取值范围;
的取值范围; 时取得极值,且
时取得极值,且 时,
时, 恒成立,求
恒成立,求 的取值范围。
的取值范围。