题目内容
(1)解方程:
(2)已知集合A=(-1,3),集合B= 集合C=
集合C= 并且
并且 ,求a的取值范围.
,求a的取值范围.
1) ;(2)
;(2) .
.
解析试题分析:(1)解对数方程,一般把利用对数的运算法则把对数方程变形为 ,转化为代数方程
,转化为代数方程 ,但解题过程中要注意对数函数的定义域,即
,但解题过程中要注意对数函数的定义域,即 ,
, ;(2)解决与集合有关的问题,我们首先应该把集合化简,本题中集合
;(2)解决与集合有关的问题,我们首先应该把集合化简,本题中集合 是不等式的解集,通过解不等式得
是不等式的解集,通过解不等式得 ,然后应用集合的运算变形转化,当集合不能直接化简时,我们还要根据集合的元素问题进行转化,例如有时转化为求函数的最值,有时转化为不等式恒成立等,本题中
,然后应用集合的运算变形转化,当集合不能直接化简时,我们还要根据集合的元素问题进行转化,例如有时转化为求函数的最值,有时转化为不等式恒成立等,本题中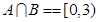 ,由条件
,由条件 得
得 且
且 ,从而求得
,从而求得 的范围.
的范围.
试题解析:(1)由原方程化简得 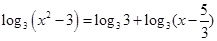 ,
,
即:
所以, ,解得
,解得 .
.
(2) ,所以
,所以 ,
,
由于 ,所以
,所以 ,所以
,所以
考点:(1)对数方程;(2)集合的运算与包含关系.

练习册系列答案
相关题目
 ,
,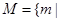 关于
关于 的方程
的方程 有实数根},
有实数根},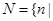 关于
关于 有实数根},
有实数根}, .
. ,
, .
. 时,求
时,求 和
和 ;
; ,求实数
,求实数 的取值范围.
的取值范围. }.
}. B时,求a的取值范围.
B时,求a的取值范围. .
. 是函数
是函数 的定义域,集合
的定义域,集合 是函数
是函数 的值域.
的值域. ;
; ,若集合
,若集合 ,求实数
,求实数 的取值范围.
的取值范围. 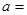
 ,且A
,且A B,B
B,B