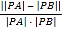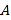题目内容
【题目】已知函数
，
.曲线
在
处的切线平行于
轴.
（1）讨论
的单调性；
（2）若
时，
恒成立，求实数
的取值范围.
【答案】（1）
在
上单调递减，在
上单调递增；（2）
.
【解析】
（1）对求导，根据题意
可得
，即可得到解析式，
在
上单增，且，可得在上单调递减，在上单调递增；
（2）令
，不等式转化为
，对
求导进行分类讨论可得实数
的取值范围.
（1）
，由题意
，
∴.∴
，
∴
，
∴在上单增，
且，∴
时，
，
时，
，所以在上单调递减，在上单调递增.
（2）令
，
即
恒成立，必有.
∵
，
.
（i）当时，
恒成立，
在
单调递增，
满足题意，所以.
（ii）当
时，由得
，
由
得
，
∴在
单调递减，在
单调递增.
又
，所以当
时
恒成立，
∴在上单调递减.
而
，∴时
与恒成立不符，
∴不满足题意.
综上所述，的取值范围.
练习册系列答案
相关题目
【题目】某小学为了了解该校学生课外阅读的情况，在该校三年级学生中随机抽取了20名男生和20名女生进行调查，得到他们在过去一整年内各自课外阅读的书数(本)，并根据统计结果绘制出如图所示的茎叶图．
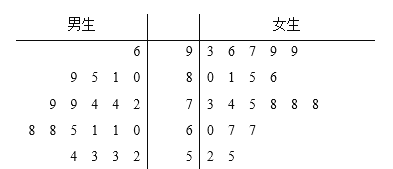
如果某学生在过去一整年内课外阅读的书数(本)不低于90本，则称该学生为“书虫”．
（1）根据频率分布直方图填写下面
列联表，并据此资料，在犯错误的概率不超过10%的前提下，你是否认为“书虫”与性别有关？
男生 | 女生 | 总计 | |
书虫 | |||
非书虫 | |||
总计 |
附：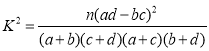
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.814 | 5.024 |
（2）在所抽取的20名女生中，从过去一整年内课外阅读的书数(本)不低于86本的学生中随机抽取两名，求抽出的两名学生都是“书虫”的概率．
