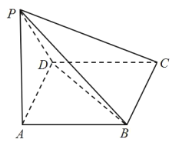
题目内容
【题目】在直角坐标系xOy中，已知直线l过点P（2，2）.以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ﹣ρcos2θ﹣4cosθ＝0.
（1）求C的直角坐标方程；
（2）若l与C交于A，B两点，求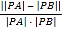
的最大值.
【答案】（1）
；（2）
【解析】
（1）把曲线
的极坐标方程两边同时乘以
，结合
，
，
，即可求出曲线的极坐标方程；
（2）由已知直接写出直线
的参数方程，把直线的参数方程代入曲线的极坐标方程，化为关于
的一元二次方程，利用根与系数的关系及参数的几何意义求解.
（1）曲线的极坐标方程为
，两边同时乘以，得
，把互化公式代入可得：
，即，所以C的直角坐标方程为y2＝4x.
（2）设直线的倾斜角为
，可得参数方程为：
（为参数），代入抛物线方程可得：
，
则
，
，
∴
，
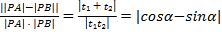
当且仅当
时，等号成立，
的最大值为.
【题目】某互联网公司为了确定下一季度的前期广告投入计划，收集了近
个月广告投入量
（单位：万元）和收益
（单位：万元）的数据如下表：
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①
，②
分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：
|
|
|
|
|
|
|
|
（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；
（Ⅱ）残差绝对值大于
的数据被认为是异常数据，需要剔除：
（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程
（ⅱ）若广告投入量
时，该模型收益的预报值是多少？
附：对于一组数据
，
，……，
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
.
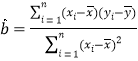
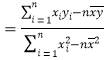【题目】某种新产品投放市场一段时间后，经过调研获得了时间
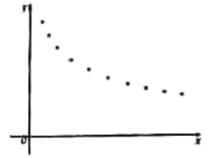
（天数）与销售单价
（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）.
|
|
|
|
|
|
|
1.63 | 37.8 | 0.89 | 5.15 | 0.92 |
| 18.40 |
表中
.
（1）根据散点图判断，
与
哪一个更适合作价格关于时间的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程.
（3）若该产品的日销售量
（件）与时间的函数关系为
，求该产品投放市场第几天的销售额最高？最高为多少元？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为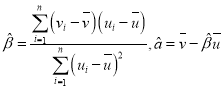
.