Question

【题目】如图①，有一个等腰直角三角板垂直于平面，有一条长为7的细线，其两端分别位于处，现用铅笔拉紧细线，在平面上移动.

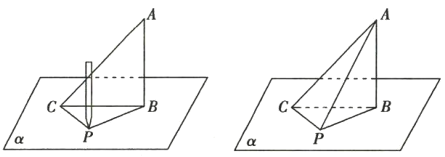
图① 图②

（1）图②中的的长为多少时，平面？并给出证明.

（2）在（1）的情形下，求三棱锥的高.

Answer 1

【答案】（1）当时，平面，证明见解析；（2）.

【解析】

（1）若使得平面，则需三角形为直角三角形且，当时，根据线面线面垂直的判定定理，证明即可.

（2）方法一，过点作于点，由（1）可知，，则平面，即为三棱锥的高，在中计算，再根据，求解即可. 方法二，设三棱锥的高为，根据，求解即可.

（1）当时，平面.证明如下：

若，则

因为，所以

所以三角形为直角三角形，且.

又因为平面平面，平面平面，平面

所以平面.

因为平面

所以.

又因为平面，平面，.

所以平面.

（2）方法一 如图，过点作于点.

由（1）知平面，平面

所以.

又平面，平面，，

所以平面，即为三棱锥的高.

由于平面，所以，

由，得.即三棱锥的高为.

方法二 由（1），知平面，平面

所以.

又，

所以，即.

设三棱锥的高为，则.

又，

且，所以，即.

所以三棱锥的高为.