题目内容
如图，在空间四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA边的中点，求证：四边形EFGH为平行四边形．
【探究】 在空间立体几何中证明某一四边形是平行四边形,首先一定要保证证明过程中证明了这个四边形是一个平面四边形,容易证明FG
DB,HE
DB,从而HE∥FG,这保证了四点在同一平面内,于是我们可以应用平面几何的有关知识证明其为一平行四边形,之后可采取证明四边形一组对边平行且相等或证明四边形两组对边分别相等的方法来证明结论.
证明：∵H、E分别为AD、AB边的中点，
∴HE
DB.
∵F、G分别为BC、CD边的中点，故FG
DB．
∴HE
FG．
故四边形EFGH为平行四边形．
【规律总结】 1.在学习立体几何命题时，要防止相关的平面几何命题引起的负面干扰．因为部分在平面几何中成立的命题，在立体几何中未必成立，因而不能盲目地将平面几何中的结论类比推广到立体几何中．对一些命题，在立体几何中被判断为真命题的，应能进行严格的证明；被判断为假命题的，只要能通过实验等途径举出反例即可．
2.本题在证明过程中容易用到在平面几何中成立而在立体几何中不成立的结论：若一个四边形的两组对边分别相等，则该四边形为平行四边形．反例如下：设菱形ABCD，连对角线AC，将△ABC所在平面与△ACD所在平面沿AC边折起，使其不在同一个平面内(得到二面角)，则该四边形显然满足四边相等，但却不是平面四边形，更不是平行四边形．
练习册系列答案
相关题目
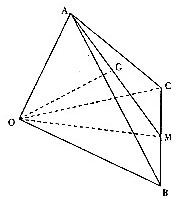如图，在空间四边形OABC中，M，G分别是BC，AM的中点，设
如图，在空间四边形ABCD中，点E、H分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且
如图，在空间四边形OABC中，已知E是线段BC的中点，G为AE的中点，若
＝
＝
，则（ ）