题目内容
设函数f(x)=kx2+2x(k为实常数)为奇函数,函数g(x)=af(x)-1(a>0且a≠1).
(Ⅰ)求k的值;
(Ⅱ)求g(x)在[-1,2]上的最大值;
(Ⅲ)当a=
时,g(x)≤t2-2mt+1对所有的x∈[-1,1]及m∈[-1,1]恒成立,求实数t的取值范围.
(Ⅰ)求k的值;
(Ⅱ)求g(x)在[-1,2]上的最大值;
(Ⅲ)当a=
| 2 |
分析:(Ⅰ)利用函数是奇函数,建立方程,即可求k的值;
(Ⅱ)对a分类讨论,确定函数的单调性,即可求g(x)在[-1,2]上的最大值;
(Ⅲ)当a=
时,g(x)≤t2-2mt+1对所有的x∈[-1,1]及m∈[-1,1]恒成立,等价于1≤t2-2mt+1在[-1,1]上恒成立,构建新函数,即可求实数t的取值范围.
(Ⅱ)对a分类讨论,确定函数的单调性,即可求g(x)在[-1,2]上的最大值;
(Ⅲ)当a=
| 2 |
解答:解:(Ⅰ)由f(-x)=-f(x)得 kx2-2x=-kx2-2x,
∴k=0.(2分)
(Ⅱ)∵g(x)=af(x)-1=a2x-1=(a2)x-1(13分)
①当a2>1,即a>1时,g(x)=(a2)x-1在[-1,2]上为增函数,∴g(x)最大值为g(2)=a4-1.(5分)
②当a2<1,即0<a<1时,∴g(x)=(a2)x在[-1,2]上为减函数,
∴g(x)最大值为g(-1)=
-1.(7分)
∴g(x)max=
(8分)
(Ⅲ)由(Ⅱ)得g(x)在x∈[-1,1]上的最大值为g(1)=(
)2-1=1,
∴1≤t2-2mt+1即t2-2mt≥0在[-1,1]上恒成立(10分)
令h(m)=-2mt+t2,∴
即
所以t∈(-∞,-2]∪{0}∪[2,+∞).(14分)
∴k=0.(2分)
(Ⅱ)∵g(x)=af(x)-1=a2x-1=(a2)x-1(13分)
①当a2>1,即a>1时,g(x)=(a2)x-1在[-1,2]上为增函数,∴g(x)最大值为g(2)=a4-1.(5分)
②当a2<1,即0<a<1时,∴g(x)=(a2)x在[-1,2]上为减函数,
∴g(x)最大值为g(-1)=
| 1 |
| a2 |
∴g(x)max=
|
(Ⅲ)由(Ⅱ)得g(x)在x∈[-1,1]上的最大值为g(1)=(
| 2 |
∴1≤t2-2mt+1即t2-2mt≥0在[-1,1]上恒成立(10分)
令h(m)=-2mt+t2,∴
|
即
|
所以t∈(-∞,-2]∪{0}∪[2,+∞).(14分)
点评:本题考查函数的奇偶性,考查函数的最值,考查恒成立问题,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
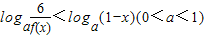 的解集.
的解集.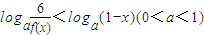 的解集.
的解集.