Question

（08年衡阳八中理）( 13分)  已知点H（0，3），点P在x轴上，点Q在y轴正半轴上，点M在直线PQ上，且满足，.

(1)当点P在x轴上移动时，求动点M的轨迹曲线C的方程；
(2)过定点A（a，b）的直线与曲线C相交于两点S、R，求证：曲线C在S、R两点处的切线的交点B恒在一条直线上.

Answer 1

解析：(1)解：设P（a,0），Q（0，b）
则：  ∴          …………1分     

设M（x,y）∵                                             

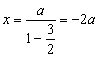
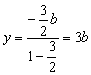∴                            …………4分      

∴点M的轨迹曲线C的方程是(x≠0) ．              …………6分  

 

 

(2)解法一：设A(a,b)，，（x₁≠x₂）

则：直线SR的方程为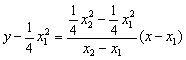：，即4y = (x₁+x₂)x－x₁x₂ 

∵A点在SR上，∴4b=(x₁+x₂)a－x₁x₂  ①                     …………8分 

对求导得：y′=x

∴抛物线上S、R处的切线方程为：

即4   ②

即4  ③                 …………11分 

联立②③，并解之得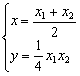 ，代入①得：ax－2y－2b=0

故B点恒在直线ax－2y－2b=0上．                             …………13分

解法二：设A(a,b)

当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点，与题意不符，可设直线SR的方程为y－b=k(x－a)

与联立消去y得：x²－4kx+4ak－4b=0             　     …………8分 

设，（x₁≠x₂）

则由韦达定理：                               …………9分

又过S、R点的切线方程分别为：，  …………11分 

故有 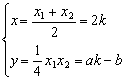（k为参数）

消去k，得：ax－2y－2b=0

故B点恒在直线ax－2y－2b=0上．                             …………13分