题目内容
【题目】已知直线l:x+2y-2=0.试求:
(1)点P(-2,-1)关于直线l的对称点坐标;
(2)直线l关于点(1,1)对称的直线方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析: (1)设出点![]() 关于直线
关于直线![]() 的对称点坐标,根据两点间线段的中点在直线
的对称点坐标,根据两点间线段的中点在直线![]() 上与两点所在直线与直线
上与两点所在直线与直线![]() 互相垂直,由中点坐标公式和两直线垂直斜率乘积为
互相垂直,由中点坐标公式和两直线垂直斜率乘积为![]() 可得关于对称点坐标的方程组,解得点的坐标;(2)设出直线
可得关于对称点坐标的方程组,解得点的坐标;(2)设出直线![]() 上任一点的坐标,利用此点关于
上任一点的坐标,利用此点关于![]() 的对称点与直线
的对称点与直线![]() 的方程,可得所求的直线方程.
的方程,可得所求的直线方程.
试题解析:(1) 设点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
则线段![]() 的中点
的中点![]() 在对称轴
在对称轴![]() 上,且
上,且![]() .
.
∴ 即
即![]() 的坐标为
的坐标为![]() .
.
(2)设直线![]() 关于点
关于点![]() 的对称直线为
的对称直线为![]() ,则直线
,则直线![]() 上任一点
上任一点![]() 关于点
关于点![]() 的对称点
的对称点![]() 一定在直线
一定在直线![]() 上,反之也成立.由
上,反之也成立.由
将![]() 的坐标代入直线
的坐标代入直线![]() 的方程得
的方程得![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目
【题目】一只药用昆虫的产卵数![]() 与一定范围内与温度
与一定范围内与温度![]() 有关, 现收集了该种药用昆虫的6组观测数据如下表:
有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求![]() 关
关![]() 的回归方程为
的回归方程为![]()
![]() 且相关指数
且相关指数![]()
( i )试与 (1)中的线性回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为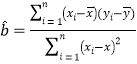 ,
,![]() ,相关指数
,相关指数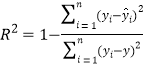 .
.
![]()
![]()
![]()
![]() 。
。
