Question

【题目】已知函数（为自然对数的底数，），在处的切线为.

（1）求函数的解析式；

（2）在轴上是否存在一点，使得过点可以作的三条切钱？若存在，请求出横坐标为整数的点坐标；若不存在，请说明理由.

Answer 1

【答案】（1）（2）不存在横坐标为整数的点，过该点可以作的三条切线.

【解析】分析：(1) 求出f（x）的导数，由切线方程可得切线斜率和切点坐标，可得a=2，即可得到f（x）的解析式；(2) 令，设图象上一点，，该处的切线, 又过点则 过作3条不同的切线，则方程有3个不同实根,进而构造，图象与轴有3个不同交点

详解：（1），

由题意可知

，，即

（2），令，

设图象上一点，，

该处的切线

又过点则 ①

过作3条不同的切线，则方程①关于有3个不同实根

令，图象与轴有3个不同交点

（1）当，，是单调函数，不可能有3个零点

（2）当，或时，当时，

所以在单调递减，单调递增，单调递减

曲线与轴有个交点，应该满足

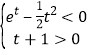，，当，又，所以无解

（3）当，或时，，当时，

在单调递减，单调递增，单调递减，应满足

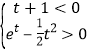，，当，又，无解，

综上，不存在横坐标为整数的点，过该点可以作的三条切线.