题目内容
在△ABC中,如果sinA:sinB:sinC=2:3:4,那么cosC等于( )A.

B.
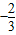
C.
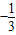
D.
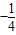
【答案】分析:由正弦定理可得;sinA:sinB:sinC=a:b:c,可设a=2k,b=3k,c=4k(k>0),由余弦定理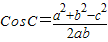 可求得答案.
可求得答案.
解答:解:由正弦定理可得;sinA:sinB:sinC=a:b:c=2:3:4
可设a=2k,b=3k,c=4k(k>0)
由余弦定理可得,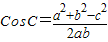 =
=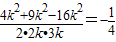
故选:D
点评:本题主要考查了正弦定理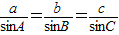 及余弦定理在解三角形中的应用,属于基础试题.
及余弦定理在解三角形中的应用,属于基础试题.
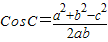 可求得答案.
可求得答案.解答:解:由正弦定理可得;sinA:sinB:sinC=a:b:c=2:3:4
可设a=2k,b=3k,c=4k(k>0)
由余弦定理可得,
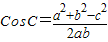 =
=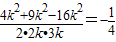
故选:D
点评:本题主要考查了正弦定理
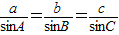 及余弦定理在解三角形中的应用,属于基础试题.
及余弦定理在解三角形中的应用,属于基础试题. 
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目